On the Tradeoffs of SSMs and Transformers
(or - tokens are bs)
This blog post was adapted from a talk I’ve given a handful of times over the last year. It was meant to be a high-level talk accessible to a fairly broad audience, but hopefully has some interesting insights, opinions, and intuitions around sequence models for the dedicated researchers too.
State Space Models
Just so we’re on the same page, I’ll start by defining what I mean by a state space model. (This section isn’t strictly necessary to get to the main part of this post though; feel free to skip directly to the next section.)
\[\begin{equation} \label{eq:ssm} \begin{aligned} h_{t} &= A_t h_{t-1} + B_t x_t \\ y_t &= C_t^{\top} h_t \end{aligned} \end{equation}\]These equations define the (structured) state space model (SSM) as developed in a line of work
The three ingredients
1. State size
A characteristic of the SSM is that its hidden state $h_t$ has a larger size than the the inputs and outputs $x_t, y_t$. The key idea is that the hidden state of any recurrent model is its only access to the model’s context (in an autoregressive setting). So for modeling information-dense modalities such as language, the model needs a large enough state to store the relevant information that it wants to access later.
In SSMs, if each input $x_t$ is a 1-dimensional scalar, then the hidden state $h_t$ is an $\mathtt{N}$-dimensional vector, where $\mathtt{N}$ is an independent hyperparameter called the state size, state dimension, or state expansion factor. This is also known as a SISO (single-input single-output) SSM and allows the models to store $\mathtt{N}$ times as much information as older RNNs such as LSTMs and GRUs
2. State expressivity
Not only does the model need to have a large enough state to theoretically store relevant context, it needs to have an expressive enough state update function to encode and access exactly the information it needs.
Earlier versions of “linear time-invariant” SSMs used simple recurrences $h_{t} = A h_{t-1} + B x_t$ whose updates are constant at every time step
This is the area with the most active research on modern recurrent models, which are focused on understanding the theoretical expressivity of different parameterizations of the transition matrix $A_t$ and what they allow the model to remember in its state.
3. Training efficiency
Having a larger and more expressive recurrent state is important, but comes with a critical trade-off – the model becomes much harder to compute. Mamba addressed this with careful parameterization of the recurrence and utilizing the classic parallel scan algorithm
Many other algorithmic innovations have appeared, all with a few shared characteristics:
- Parallelization: They aim to be parallelizable and practically efficient on accelerators like GPUs and TPUs – preferably leveraging matrix multiplications (matmuls) as the workhorse.
- Memory management: They have to control memory usage carefully. In particular, any model that uses state expansion can’t actually materialize the state in main memory! While Mamba brute-forced the problem using clever awareness of the GPU memory hierarchy
, most alternatives find ways of rewriting the equations entirely to use different computation paths that don’t need to compute the state explicitly during a parallel training pass. - Linearity: The model generally has to be linear in $x_t$, leading some to call this whole family of models linear recurrent models. Linearity plays a role in both computational efficiency as well as modeling/optimization ability, which I won’t get into here.
Mamba - putting it all together
None of these three ingredients is new:
- Linear attention
and earlier SSMs had similar equations utilizing state expansion. - Selectivity was inspired by, and closely related to, gating mechanisms in classical RNNs like the LSTM and GRU
. - Parallel scans were utilized in earlier SSMs/linear RNNs like S5
and LRU . Linear attention variants also used parallelizable training algorithms leveraging matmuls.
What Mamba did was show that combining all of these together was the key to a step change in empirical performance and approaching Transformers on language modeling.
Modern recurrent models
Since then, there’s been a flurry of activity on continuing to understand and improve recurrent models. Many of them come from different motivations with different nomenclatures and terminologies.
- Some models such as RWKV
, xLSTM , and Griffin come from an RNN-centric point of view and call Ingredient 1 matrix-valued states and Ingredient 2 gating. - Linear attention
first combined Ingredients 1 and 3; later variants such as GLA and Gated DeltaNet incorporate various forms of selectivity (data-dependent recurrence) and use attention-based terminology such as using $(K, Q, V)$ instead of $(B, C, X)$. Mamba-2 can also be simultaneously seen as either an SSM or a linear attention . - Recently, many of these models have been cast into a framework of test-time training/regression
, which views the recurrent update as online optimization on some objective for remembering the context. The state is viewed as an associative memory and parallelization happens through a notion of minibatch gradient descent.
A core commonality is that almost all of these models can be cast into the same SSM equation \eqref{eq:ssm}, with the main axes of variations being in the structure of $A_t$ (Ingredient 2) and corresponding efficient training algorithms (Ingredient 3). So I’ll use the term state space model (or just “modern recurrent model”) to refer broadly to this large class of new models, as it captures their main shared characteristics (e.g. SISO linear recurrence with state expansion). But of course, there are many other reasonable names given the closely related ideas!

Despite the accelerating amount of research into this direction and steady stream of new models, however, I think that all of them are still quite similar to each other and have roughly similar empirical performance, for the most part. In particular, all of these models are much more similar to each other than they are to quadratic attention. So in the rest of this post, we’re going to try to get a grasp on the higher-level tradeoffs between SSMs and Transformers.
States, Databases, and Brains
I claim that we can understand the trade-offs of different models better by looking at what they store in (and how they manipulate) their autoregressive state.
What does that mean? In some sense, every autoregressive model – one that generates data sequentially left-to-right like modern LLMs – is a “state space model” that holds some state in memory and evolves it on every time step (e.g. in between every generated word for an LLM).
Autoregressive states of sequence models
(Causal) self-attention, the core component of autoregressive Transformers, is often defined through a specific operation involving computing the pairwise interactions between every element of the sequence
On the other hand, because computing one step of the recurrence \eqref{eq:ssm} takes constant time, processing an entire sequence scales linearly with the length of the sequence, which is often viewed as the main advantage of state space models.
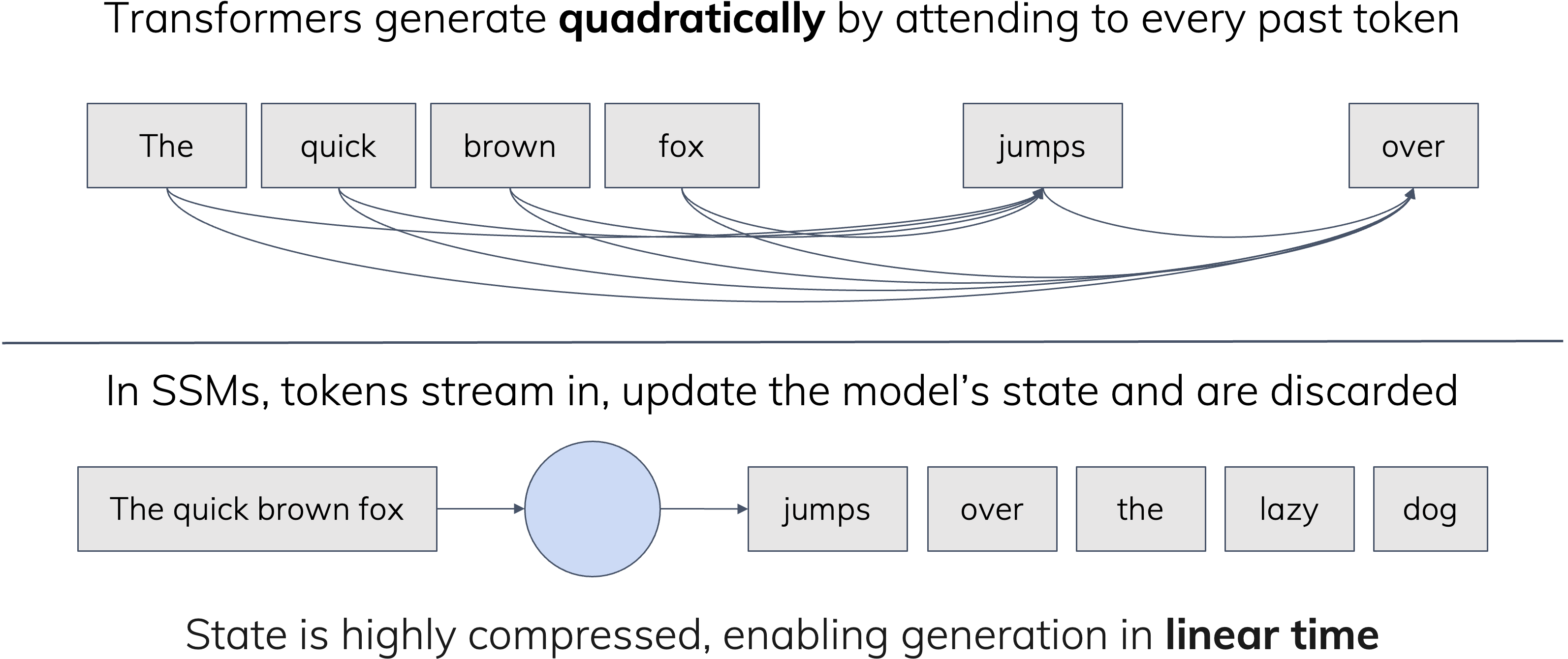
But instead of thinking of the training cost of these models, I find it more illuminating to think about what happens at inference time when they process a new input.
- When a self-attention layer receives a new token, it needs to compare it to all the previously seen elements of the sequence, which means that it must have cached a representation for every single prior token in the context. Every new input it sees must get added to the cache, which therefore grows linearly in the context size.
- On the other hand, a state space model has always summarized its context $x_1, \cdots, x_t$ into the hidden state $h_t$ (equation \eqref{eq:ssm}), which always has a constant size. This fixed-size state is the only means by which the model can interact with data: it streams data in, compresses it into its state, and uses that to make decisions or produce new outputs.
Without even getting into the details of the definitions of these various models, I think it’s roughly accurate to say that we could have defined them from first principles through their autoregressive states:
- Transformers (self-attention) are characterized by a state that caches every element of its history, and interacts with new data by doing a pass over every element of the cache.
- SSMs are characterized by a state that compresses all its history, and interacts with new data in an online streaming fashion.
Aside: The “KV” cache
The Transformer cache is, of course, more formally known as the KV cache, where “KV” refers to specific parts of how attention was first defined and named (key and value).
But the point of this description is that I think that rather than defining the KV cache as a consequence of attention; perhaps in an alternative universe, (causal) self-attention could have been derived from first principles as the canonical model that stores a cache (“KV” or not) of its context. So in this post, I mainly call it a “context cache” or “token cache” instead to abstract out the main principle instead of implementation detail.
As an aside, it’s rather interesting/amusing to me that often when I talk to LLM researchers, they call the recurrent state of SSMs a “type of KV cache” rather than calling the KV cache a type of state, which IMO is much more accurate and descriptive.
A coarse analogy
Although SSMs are often viewed as more efficient but somewhat weaker versions of Transformers, it’s not as simple as that. Even ignoring computational efficiency, these models do have different tradeoffs in their inductive biases (or modeling power). Given the nature of the way they process data, here’s a rough analogy that I like.
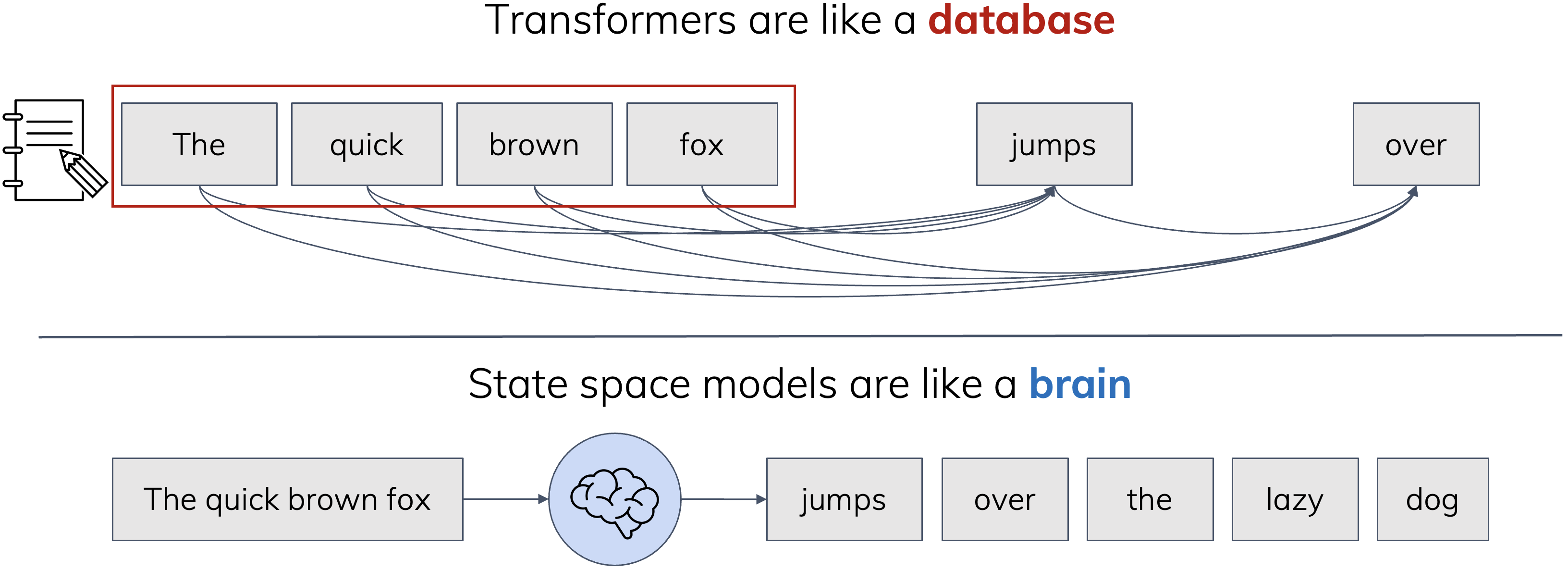
Transformers are like databases: they treat every new observation as an important item that is filed away for future reference.
On the other hand, SSMs are like brains: finite-sized memories that are always on, processing new inputs and producing new outputs in real-time.
This analogy is a bit superficial, but does help intuitively explain some of the empirical behaviors that are observed. For example, SSMs can’t memorize a phonebook in one pass and then recite it back, or recall an arbitary person’s phone number from memory
Aside: Context compression
The aforementioned limitation on context length might be circumvented by newer context compression techniques, which involve a more clever iterative process of throwing out the entire cache and trying to compress it into a shorter summary, so that new information can be processed that otherwise would overflow the cache. This of course must be lossy, and makes the whole system start resembling an SSM more.
Similarly, the limitations of SSM may be alleviated by more clever iterative techniques of interacting with the data. For example, issues with recall might be remedied by giving them another pass over the data – just as how humans will look things up in external references.
The theme here is that sometimes limitations of methods are not so black-and-white. They can depend on the way in which models are used and more generally on higher system-level changes. But we’re not going to get into these nuances for the purposes of this post.
Aside: Long context
Something worth pointing out is that “long context” is a very popular, but horribly overloaded and ill-defined term. Both Transformers and SSMs have been touted as having better “long-context abilities” as a blanket statement, which can’t both be accurate.
The reason is because they have very different types of memory. Going back to the analogy, I wouldn’t say that there is a clear winner comparing, say, my own memory vs. my research notes. They’re both just different: my notes lets me refer back to specific details I may have forgotten, but my brain remembers a much longer history of fuzzy context. Transformers and SSMs probably have similar qualitative differences that are difficult to measure.
I’m very curious, for example, if large-scale SSMs (if trained properly with modern length extrapolation techniques

A more intriguing empirical finding that might be predicted from the analogy is that combining both types of information processing may be even more capable! Just as human intelligence is augmented by having explicit scratch pads and external references, language models get better when combining SSMs with attention layers by a simple interleaving strategy.
And what’s even more intriguing is that the optimal ratio of these layers, as independently verified by dozens of research groups by now (H3, Jamba, Zamba, Samba, and many more that followed after)
Aside: Perplexity
When I talk about performance here, I’m specifically referring to perplexity. As a community, we now know that there are more nuances to the downstream performance, in particular algorithmic capabilities of different types of models
I actually believe that pound-for-pound (or FLOP-for-FLOP), SSMs are better than Transformers at modeling language, in this sense. But of course, there are many other downstream capabilities that have other differences and are important to understand.
Is Attention All You Need?
So attention is all you need, right? There’s a perception of Transformers being the ultimate architecture that can learn anything from raw data, the more the better, with having enough compute being the only bottleneck.
Myth
Just throw your data at a Transformer 🙂
Well, not quite. Attention is indeed amazing and has become an effective backbone for pretty much all modalities, from its original applications in language to vision and audio and beyond
Reality
Attention is most effective on
pre-compressed data at the “right level of abstraction”
I claim instead that in order to use a Transformer effectively, the data has to be substantially processed. To support this claim, let’s look at how they’re actually used in practice.
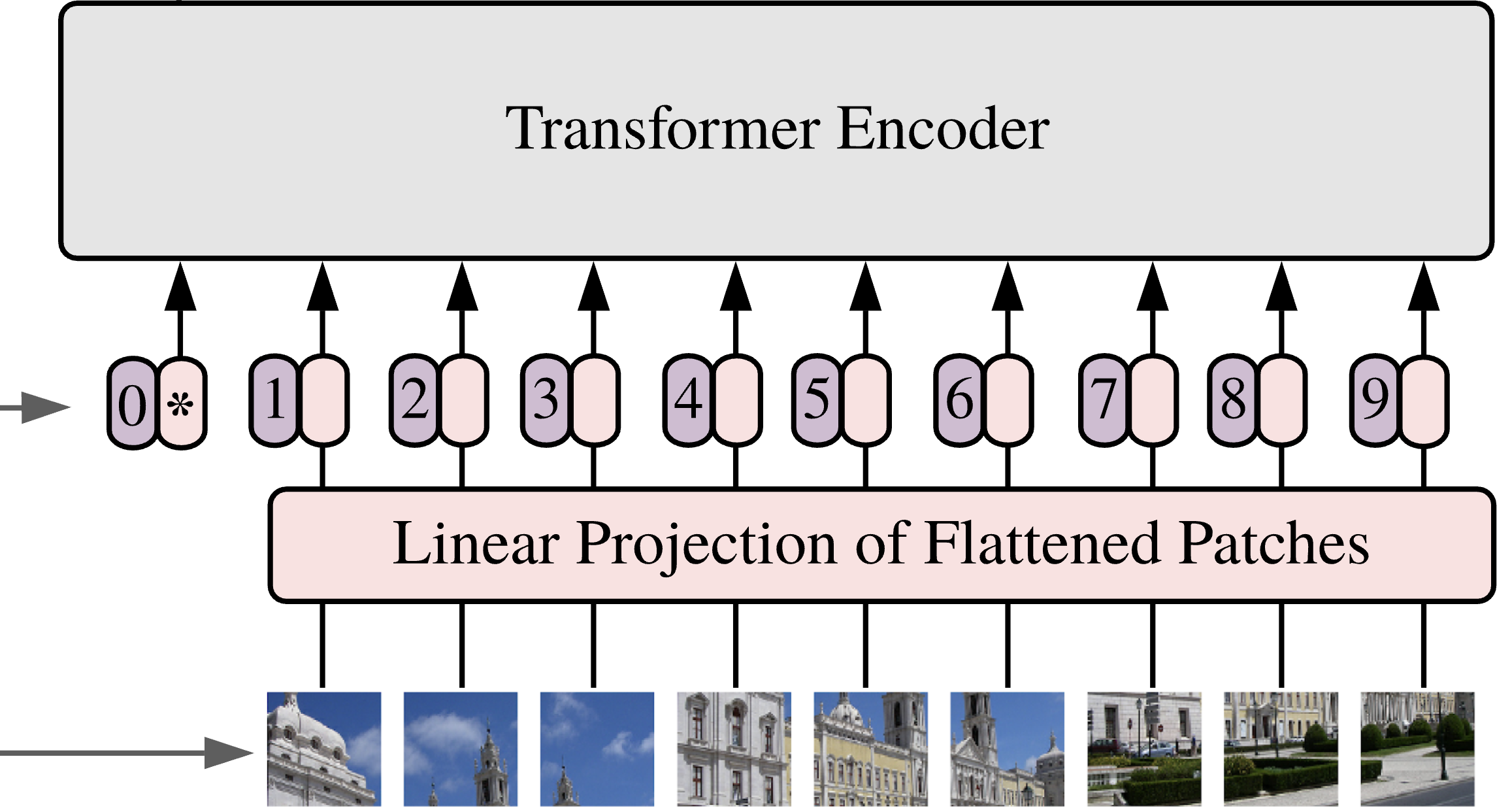
In pretty much all real pipelines, raw data is processed by an encoder before being fed to a Transformer, for example:
- The patchification step in vision pipelines (whether classification or generation)
. - The tokenization step of language modeling.
This may seem intuitive: after all, because of the quadratic complexity of attention, of course it makes sense to try to simplify the data (such as shortening input sequences).
But my claim is not just about computational efficiency; I’m making a stronger statement about limitations in modeling power.
Let’s dig in more here.
Should we get rid of tokenization?
Tokenization is a notorious step of all language modeling pipelines (most commonly the “BPE” algorithm

So why do we use it?
From polling a lot of opinions, almost everyone agrees that tokenizers are clunky and ugly, but a “necessary evil”.
I, on the other hand, deeply believe that we should get rid of tokenization. I’m driven by aesthetics much more than the average person, I’d guess, and it’s because I think that they are rooted in intuition and intangible reasons that usually lead to deeper consequences down the line, even if we can’t predict them. Indeed, an example is all the work I’m now known for on RNNs/SSMs, which only became useful after years of work, which stemmed from an aesthetic conviction that recurrence is elegant and fundamental. In this case, I think that the consequences of overcoming tokenization will extend far beyond the surface-level implications.
We should care about removing tokenization, not (just) for the practical reasons, but for the aesthetic and intangible reasons.
Besides fixing the edge cases, removing tokenization simply adheres closer to the spirit of deep learning. Deep learning has always been about replacing handcrafted feature engineering with powerful end-to-end neural networks that can learn patterns automatically from data. From CNNs replacing manually engineered edge detectors in computer vision, to Transformers replacing linguistic features in NLP, major advances in AI have always happened with less data processing and more automatic learning (as popularly espoused by The Bitter Lesson)
I believe that replacing tokenization with end-to-end models will have huge consequences for
- scaling laws: learning better patterns from raw data always leads to more powerful models;
- multilingual and multimodal: tokenization is notoriously hard or impossible for certain languages and other types of sequential data;
- reasoning: because models can learn more semantically meaningful patterns from the data, and reason over higher levels of abstraction;
and much more, some of which I see and some of which I haven’t thought of yet.
(As I was writing this post up, Luca Perić released a parallel blog post focused specifically on tokenization and tokenizer-free architectures. Check it out!)
So what happens without tokenization?
In the modern era of LLMs, there’ve been astonishingly few papers that have thought about or tried to address this problem. It’s hard to even find trustworthy benchmarks about the performance of tokenizer-free models.
So here’s a plot from our upcoming paper where we carefully ran standard architectures on byte-level language modeling (essentially, treating each English character as a separate token). (Note: Byte-level modeling with Mamba was first attempted by MambaByte
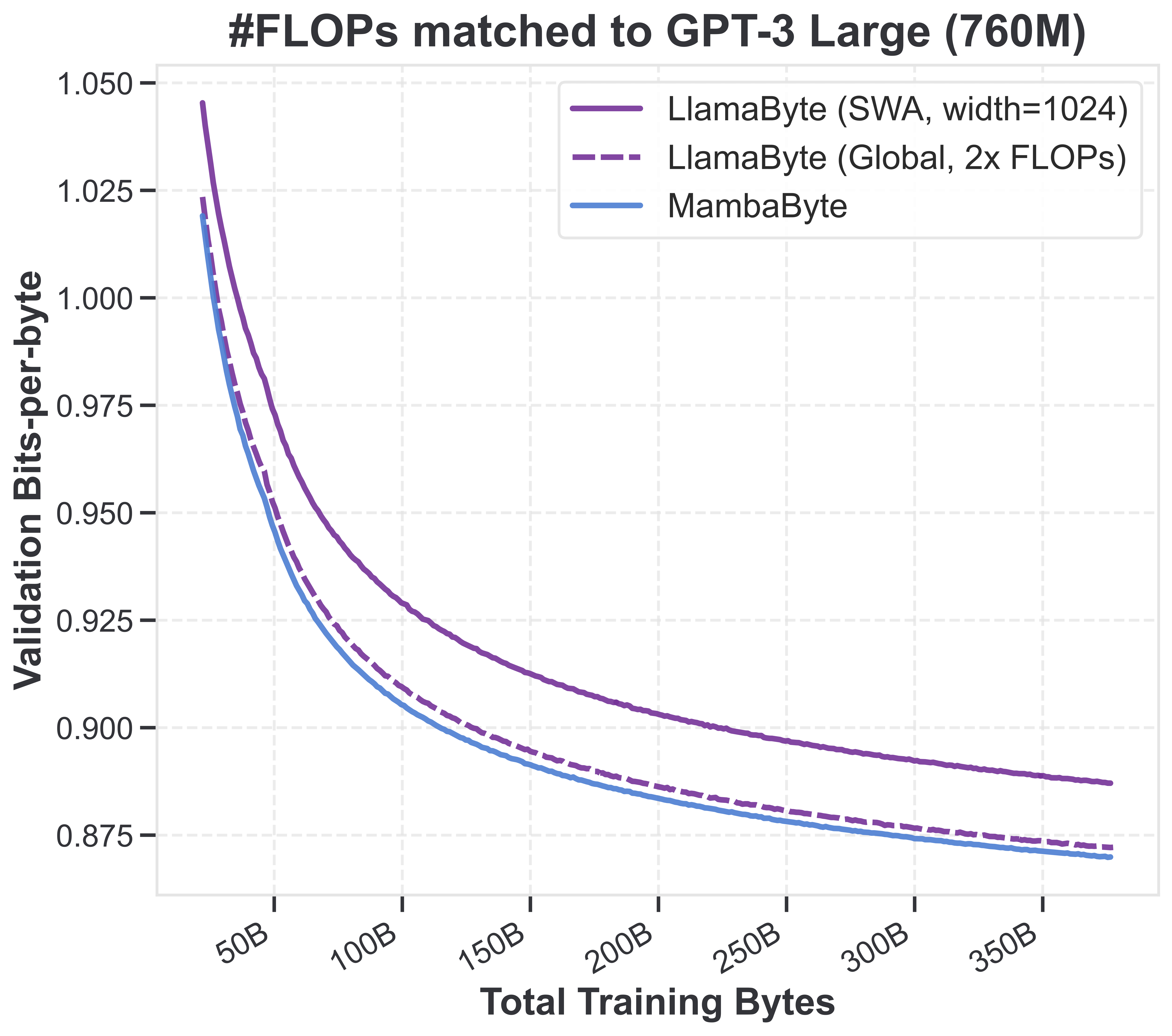
There are a number of implications here that most LLM researchers seem to find surprising.
The first thing to note is that the SSM performs much better than the FLOP-matched Transformer. This might not seem that surprising because byte sequences are much longer than BPE-token sequences, and the quadratic complexity of Transformers kicks in.
But as I said earlier, the weakness of Transformers is not just about efficiency, but about modeling power. And what’s notable about this plot (in particular, focusing on global attention) is that when matching for data instead of compute, allowing the Transformer to use many more FLOPs, the SSM still outperforms it consistently!
For contrast: if we compared these models on the exact same data, but tokenized
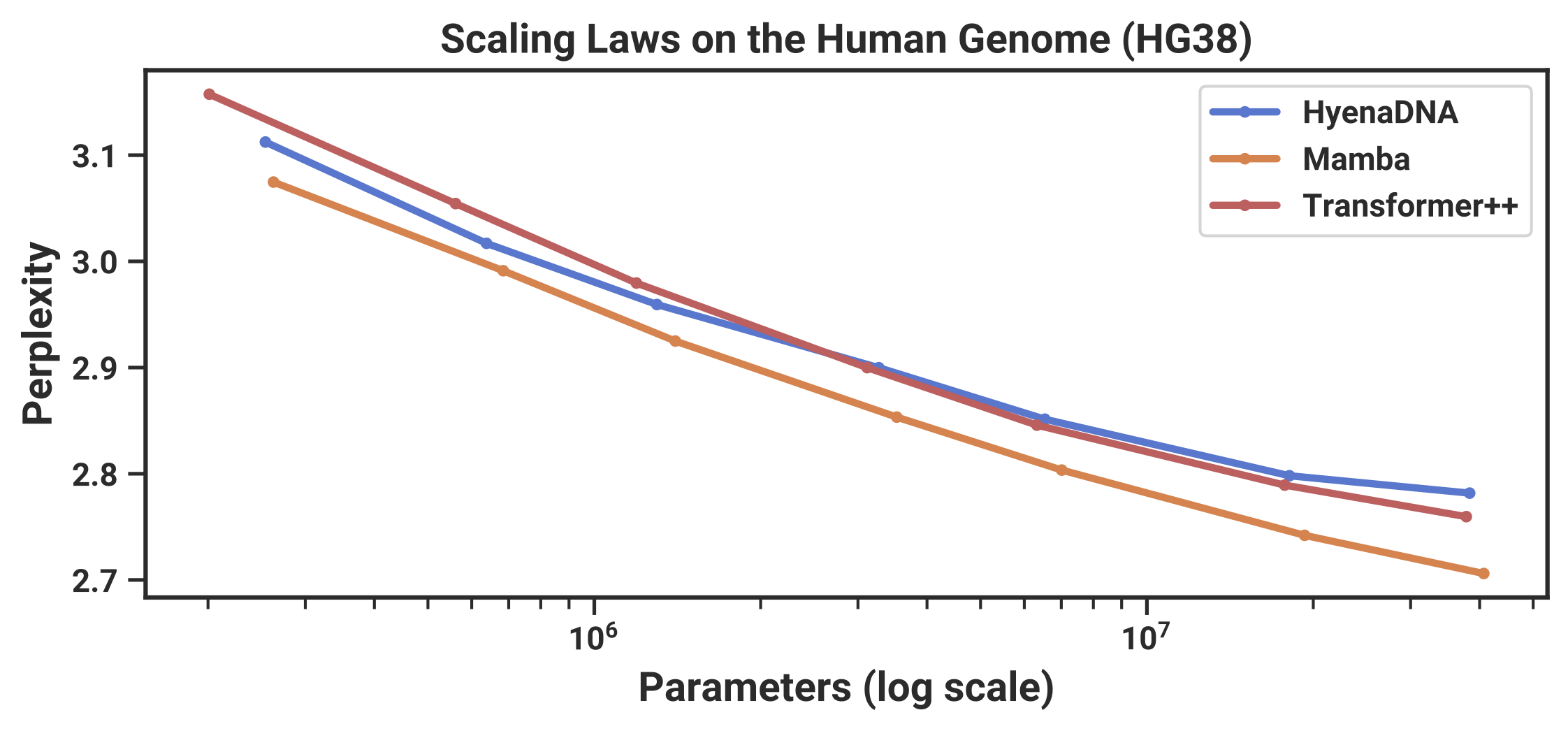
Here’s another example. This plot is from the original Mamba paper, where we showed that Mamba scaled substantially better than Transformer out-of-the-box on DNA language modeling. Once again, this is a “tokenization-free” language with high-resolution input and small vocabulary size (just 4!), and the SSM strongly outperforms the Transformer when data-matched (while using less compute).
(By the way, I hypothesize that these results for tokenizer-free models would hold for any reasonable variant of SSMs, such as probably most of the [modern recurrent models].)
A heuristic explanation
A useful model of what’s happening is to turn back to the autoregressive state. In a nutshell, because Transformers have an explicit cache of all prior tokens, they have an inductive bias to pay attention to individual tokens.
The inductive bias of soft attention is hard attention.
Here are some useful heuristics for when attention is naturally suited to the task:
- Does caching a representation for every “token” of data make sense?
- Does hard attention (focusing on or recalling an individual token) make sense?
These questions point at the following idea: is each individual token semantically meaningful? For example, when reading language, we pay attention to units at the level of words (or subwords like prefixes/suffixes), which have meaning. But on the other hand, when this doesn’t hold – for example, it’s rare that we’d ever want to pay attention to an individual character when reading – the performance of attention suffers.
What’s interesting is thinking about many other types of data which lie somewhere in between. For example, image patches can be quite meaningful when they capture some feature, but often can be useless or only partially meaningful.
| Data | Is a token “meaningful”? |
|---|---|
| Words / subword tokens | |
| Characters | |
| DNA base pairs | |
| Image, video, audio patches | |
| Time series datapoints |
This is why I do think that attention is indispensable for data like tokenized language, which has largely been processed to a degree of meaning.
On the other hand, when the data is generally not meaningful (in the sense of requiring a model to pay attention to individual units), such as character-level language or DNA
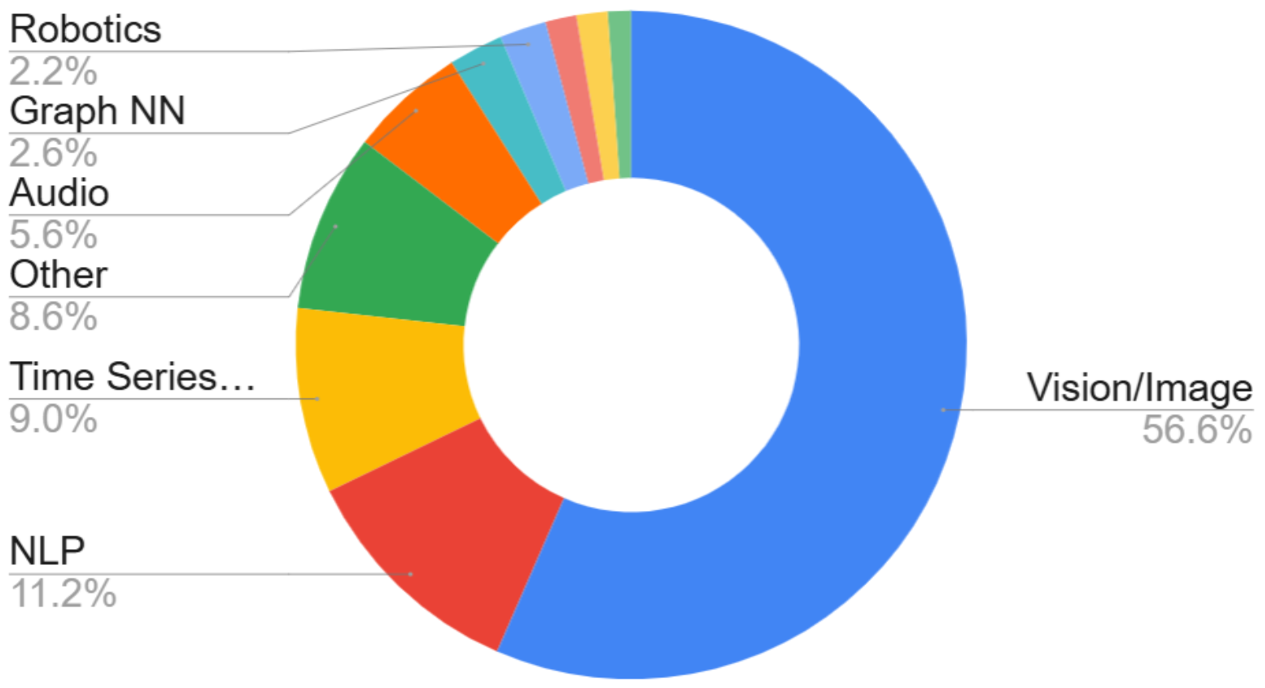
The above figure, which was helpfully sent to me by the hosts of The Cognitive Revolution podcast, shows the breakdown of where Mamba was actually used after being published. Despite being motivated by and focusing on language modeling in the paper, the majority of its applications were actually in other modalities!
These heuristics are, of course, very unrefined, and I’m sure many researchers would take issue with this depiction. But I’ve found it helpful for intuition and has been pretty good at predicting when various models are effective in practice.
Aside: Theories of tokenization
As people start thinking about tokenization more, there are some interesting theoretical results that have emerged which support this central thesis (that Transformers require meaningful tokens).
-
Tokenization Is More Than Compression examined the hypothesis that the primary role of tokenization is to shrink the input sequence length. They invented a new tokenizer that has even higher compression rates than BPE (actually, they even keep the same vocabulary, but simply find different segmentations that are more compressed) yet leads to worse language models, providing evidence against the hypothesis
. -
An Analysis of Tokenization: Transformers under Markov Data showed that for certain data distributions, applying tokenization qualitatively changes what Transformers can learn. Intuitively, commonly used tokenizers like BPE and Unigram are somewhat based in information-theoretic heuristics, and play a particular role in smoothing out the non-uniform information rate of raw data into a form that’s more easily processed by a Transformer
.
Aside: Do SSMs not need meaningful input?
Of course, working on more meaningful inputs would benefit all models, not just Transformers. But I hypothesize that Transformers particularly rely on it.
In one of the iterations that I gave this talk, an audience member asked me the question of what I thought would happen if Transformers or SSMs were run on “$n$-gram tokenized” language (instead of using BPE tokens, divide up the text into fixed windows of $n$ characters) or some other suboptimal tokenization.
I predicted that both models would get worse on poorly segmented data, but it would affect SSMs less: in order of performance,
Transformer (bad tokens) < SSM (bad tokens) < SSM (good tokens) <= Transformer (good tokens)
Byte/character-level modeling (equivalent to $n$=1) certainly provides some evidence for this.
A hypothetical litmus test
Another thought experiment that’s intrigued me is what happens in the presence of noise. LLM data notoriously requires immense amounts of processing, filtering, and cleaning, but real-world data (and other modalities) aren’t like that. Humans also learn just fine from noisy data!
So, what happens in a very simple scenario where information-less filler tokens are inserted into the sequence?

This figure illustrates a redundancy factor of $2\times$, but of course this can be arbitrarily increased to $k\times$ in the thought experiment. I think this shows another clear failure mode of standard attention: the compute shouldn’t be scaling as $k^2$, and the (inference) memory certainly shouldn’t scale in $k$ either – caching the noise tokens is pointless.
SSMs are much better: as $k$ increases, the memory doesn’t grow. But it actually doesn’t fully fix the problem either, as any standard architecture would have compute scaling with $k$ (since every token is processed by the entire model). And so all LLMs suffer from this sort of noise and redundancy.
In fact, I think thought experiments like this provide useful litmus tests for what “the right architecture” should look like. And I’ll informally propose this one as a goal for the future of architecture design (maybe someone will help me formalize it in a paper someday?).
A Litmus Test
An ideal architecture should be able to process this sequence-with-fillers task without (substantially) increased compute or memory usage.
More generally, suppose we have two copies of a dataset, one of which contains a lot of extra noise, but overall they have essentially the same “information content”. We should expect “the right architecture” to behave essentially identically on both of these data sets.
Aside: Convolutions for language modeling
On a somewhat tangential note, I originally came up with the thought experiment in the figure above years ago, as a means to convince myself that convolutions don’t work for language modeling. When S4 was published, the community was excited about its potential on various modalities, and it spawned a wave of follow-up work on pure convolutional language models
But over the course of working on linear time-invariant SSMs, I quickly realized they were hopeless for language modeling. This example shows why: because language doesn’t have an intrinsic “sampling rate”, tokens can be spaced somewhat arbitrarily. Clearly, even simple mis-spacings would drastically change what features a convolution could pick up on – in the above example, the convolution could not possibly output the same feature on both of those input sequences, in contrast to input-dependent sequence mixing layers like attention or selective SSMs.
On the other hand, convolutions exhibit strong inductive bias exactly when there’s a notion of sampling rate that spaces inputs out at a consistent rate. This is another way of phrasing the “shift equivariant” inductive bias that makes them so great for (raw) perceptual modalities like vision and audio.
Is attention all you need? (redux)
So through these discussions and examples, hopefully I’ve made a case for my original claim, which I’ll repeat here:
Attention is most effective on
pre-compressed data at the “right level of abstraction”
This is, of course, an oversimplification of the picture – and I wouldn’t even know how to try to formally define a “level of abstraction” – but I do believe this is true in some fuzzy sense.
The Tradeoffs of State Space Models and Transformers
Let’s finally return to the main topic for this blog post.
State space models
The trade-offs of SSMs are pretty clear from thinking intuitively about its autoregressive state.
The Strength
SSMs are the natural stateful model with efficient, interactive, online processing.
The Weakness
SSMs lack fine-grained recall and retrieval abilities.
Both of these are two sides of the same coin – consequences of its compressed state.
I want to note, however, that I think there are strengths that are more subtle, and difficult to measure or even articulate.
Going back to the [brain analogy], one question that intrigues me is whether compression is actually fundamental to intelligence.

At any rate, there are certainly many interesting applications where SSMs are the right tool for the job right now. And in my lab’s next release, we’ll show another interesting and important use case (for language!) where the compressive inductive bias of SSMs turns out to be essential. Stay tuned!
Transformers
Transformers perform exceptionally well, and in fact are pretty much the only tool for the job, on tasks that require paying attention to individual tokens in the context.
The Strength
Transformers have perfect recall and fine-grained manipulation of individual tokens in their context.
And what about the downsides? Everyone knows that the main weakness of Transformers is their quadratic complexity, right?
Not exactly. The main theme of this post is to convey that Transformers do have inductive biases that gives them weaknesses in terms of modeling power, not just efficiency. And just as with SSMs, both the high-level strengths and weaknesses of Transformers are two sides of the same coin, consequences of the structure of their autoregressive state: the token cache maintains the granularity of the input resolution it’s given.
The Weakness
Transformers are beholden to the tokens they are given.
In other words, they are more sensitive to the resolution and semantic content of the data. Transformers are characterized by their context cache, which stores a separate representation for every element of the sequence, which means that every element better be useful.
Aside: What about efficient attention?
Many variants of attention exist, which have been primarily motivated by the efficiency angle. I think my framing gives us better intuition of how these variants might behave. For example, I hypothesize that the same weakness is present for any variant of attention that maintains an explicit token cache; in particular, for example, any type of sparse attention. The core weakness is still there (and perhaps even exacerbated in the case of sparse attention): the model is biased toward attending to individual tokens.
On the other hand, some variants of efficient attention “blur” the boundaries of tokens, including low-rank approximations
Incidentally, this is another more subtle reason why I somewhat prefer using “state space model” or “recurrent model” as a descriptive term over “linear attention”.
Scaling Laws
To end, let’s talk about one of the major drivers of the current wave of progress in AI:
scaling laws, or the phenomenon that spending more compute on models consistently leads to more capabilities.
These laws are always plotted with FLOPs on the x-axis and some measure of performance on the y-axis, with the idea being that the slope of this line measures “the rate at which compute is converted into capabilities”. Indeed, I think there’s a popular viewpoint that Transformers are simply a vehicle that optimally performs this conversion.

And I think this is a great depiction of the goal of architecture research. We’re simply looking for the black box that performs this conversion in the best way possible. From this perspective, there is only one central question:
Is my model using its compute wisely?
In other words, we want every FLOP to count. And as is hopefully clear after this post (at least, I’ve convinced myself!), Transformers are far from optimal.
Aside: Does it actually matter?
There’s another layer to the picture that I haven’t touched on, which is the practical efficiency of models. As Tri likes to frame it, what we actually care about is “dollars-to-capabilities”, which can be factored into (1) “dollars-to-FLOPs” and (2) “FLOPs-to-capabilities”. One might need to balance these two, for example, by accepting a suboptimal architecture for (2) in return for much more efficient (1). And some might say that Transformers have optimized the combination of these two.
I still care primarily about question (2), partly because I personally find it more intellectually interesting, but also because I truly believe there are substantial advances to be made that change the balance even factoring in (1).
A second higher-level question touching on whether it actually matters is: do we need to improve on anything to get to AGI/ASI? The answer here might be no – tokenized Transformers may very well represent a viable path – but I think that finding improvements may either get us there faster, or ultimately lead to more intelligent models.
Don’t get me wrong: despite being known as a leader of the Transformer-alternatives direction, I think Transformers are amazing and attention is truly a fundamental modeling primitive. But I also think it’s clear that they, by themselves, are not the final solution. We still have work to do.

What’s next
Part of my reason for writing this post was to broadcast this content to a wider audience, and so this talk can be sunsetted :)
But it’s also setting up for the next major architecture advancement…
Acknowledgements
Thanks to Tri Dao and Luca Perić for feedback on this post.
The MambaByte vs. LlamaByte plot is from Sukjun Hwang from his H-Net paper (blog).
Cite this post
@online{gu2025tradeoffs,
author = {Albert Gu},
title = {On the Tradeoffs of State Space Models and Transformers},
year = {2025},
url = {https://goombalab.github.io/blog/2025/tradeoffs/},
}