H-Nets - the Past
This post is part of a two-part series.
- H-Nets: the Past
- H-Nets: the Future
The H-Net model has been a dream of mine for years. I’ve been fortunate enough to be able to work with my student Sukjun Hwang who made the technical breakthroughs behind this model, solving (or at least making serious progress towards) what I consider to be a very difficult but foundational problem for deep learning.
In this post, I provide an informal personal recounting of the motivation and history of this project, adding various context and discussion that wouldn’t make sense in a paper. This post is really just for fun; I’ve always found it interesting to read about the windy history of research instead of just the streamlined final result, and I felt like telling this story.
In the next post H-Nets (the Future), I’ll explain why I think this model is so important and a variety of potential downstream implications.
This series of posts can also be seen as a followup to my previous post on the tradeoffs of SSMs and Transformers, which may help contextualize this model.
Hierarchy is Everywhere
The idea of hierarchy has always resonated with me. Perhaps its comes from my penchant for discrete math and roots in competitive programming, where I spent all day working with algorithms on trees, the canonical hierarchical structure. Perhaps it reflects the way I tend to think; I structure almost everything hierarchically, for example using bulleted outlines for everything to a perhaps excessive degree (I’d write papers in outline format if I could!).
At some point early in my PhD, when I wasn’t doing much productive work, I took an online class for fun called Learning How to Learn. I think this is where I came across the concept of chunking in human cognition, which really resonated with me and felt fundamental to intelligence. For example, our processing is strongly hierarchical: language is parsed into words, phrases, clauses, sentences, and beyond; perception is organized into objects and events; tasks are decomposed into subtasks and goals. Raw streams of thought are chunked into abstractions and ideas. The chunking concept seemed really important to me, and later became adopted for this project’s terminology.
Hierarchical RNNs
From the very beginning of my work on sequence models, I was drawn to hierarchical models.
My first exposure to sequence models came during an internship in 2019 at DeepMind under the amazing Caglar Gulcehre and Nando de Freitas. I started thinking about RNNs with help from Caglar, who was an encyclopedia of classical sequence models (e.g. he was on the original GRU paper
I was particularly interested in the idea of improving long-range dependencies through hierarchies. This had been attempted in many flavors of older RNNs, such as the Clockwork RNN
S4 and SaShiMi
After DeepMind, my research switched completely to sequence models
Autoregressive U-Nets for image modeling

In this paper, we tested S4’s autoregressive modeling ability on a variety of distributions: on the left is the CIFAR-10 density estimation problem, and on the right is language modeling on WikiText-103 (at the time a popular dataset, but far too small scale now).
To improve the pixel modeling problem performance, I actually introduced an autoregressive U-Net structure that had two stages of downsampling. The overall structure of this model, such as the fixed-width pooling and how to preserve causality for the autoregressive sampling, is very similar to a bunch of models that have since been used for language (such as Hourglass Transformer, MegaByte

As far as I’m aware, this paper (concurrently with Hourglass Transformer
U-Nets don't work for language
Something not reported in the paper, though, was that I tried the same backbone on the WikiText-103 language modeling experiments as well. I really wanted it to work, since I felt like hierarchy should be important! But no matter what I did, the hierarchical version was always noticeably worse than the isotropic backbone for language modeling.
I eventually gave up on this, and I think it formed the basis for some of my intuition around language modeling. In particular, I realized that fixed-width pooling just didn’t make sense for language. (And moreover, I realized that this is essentially the same as convolutions, or at least has the same inductive bias, and this helped form the basis of my hypothesis about how convolutions don’t work for language modeling or more general “discrete data” that has variable spacing. See this part of my Tradeoffs post for a bit more discussion.)
To be honest, I don’t really understand how so many papers on this U-Net-like strategy have been published for language modeling. I’m pretty skeptical that they work at all, as has also been shown in ablations by follow-up works on byte-level language modeling like SpaceByte
But they work great for audio!
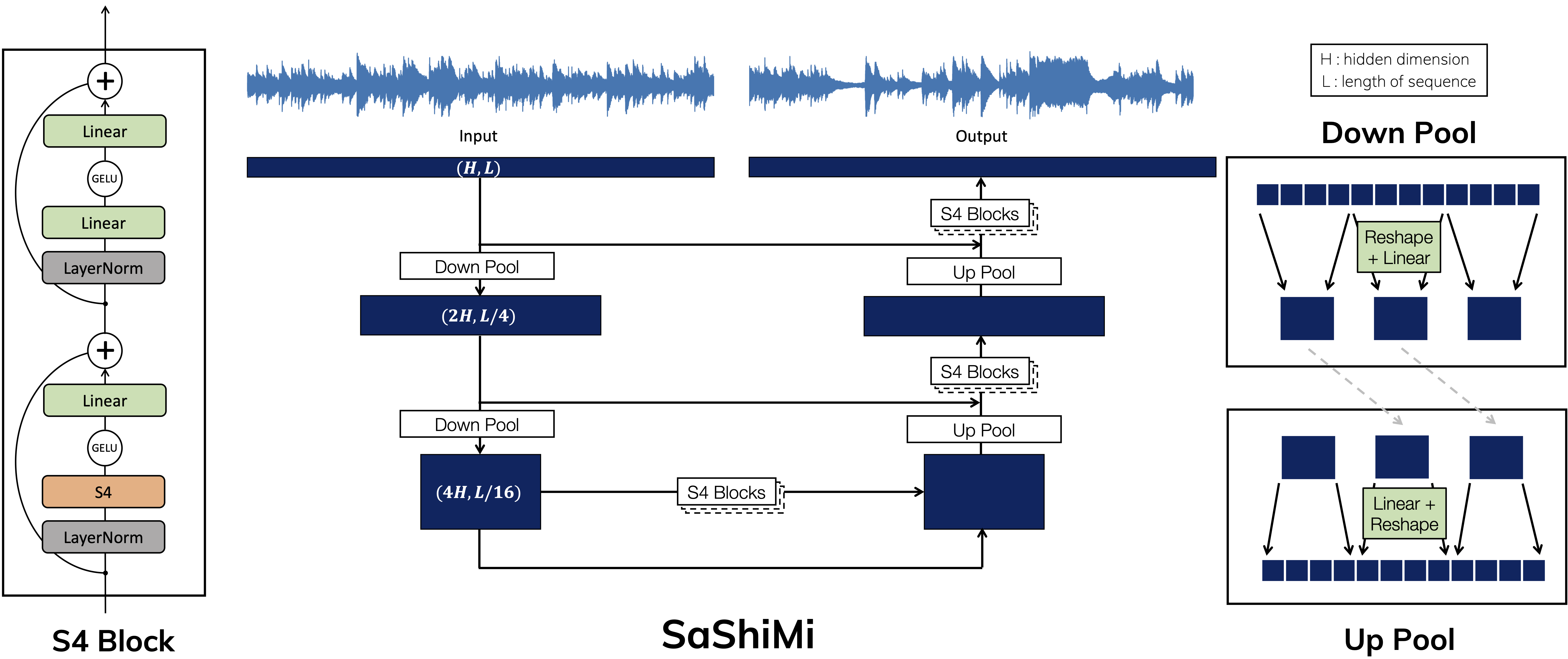
Instead, I realized that S4 and U-Nets (and convolutions in general) have a great inductive bias for data that has an underlying notion of uniform sampling rate, namely perceptual modalities like audio, images, and video. So Karan took this autoregressive U-Net backbone with S4 layers and applied it to modeling/generating raw audio waveforms, where it worked really well
A Differentiable Chunking Mechanism?
Around 2022-2023, I was idly thinking about hierarchies in the back of my mind, and the way I conceptualized the goal was something like this.
Attention as a primitive
To me the self-attention mechanism could be phrased as: A basic module that captures the “primitive” of forming dense connections and building functions on sets. What makes it powerful is that it feels simple and foundational - capturing some fundamental transformation in a simple differentiable way that allows it to be scaled.
My research is always after these primitives: lower-level building blocks that capture fundamental properties and transformations, and can be flexibly applied and scaled. The work I did for years on RNNs and state space models, for example, is really about fleshing out the primitive of recurrence, which I also do view as being a fundamental property of the world. (It’s probably not a very well-known fact that my academic job talk was not about SSMs per se; it was called New Structured Primitives for Machine Learning!)
Chunking as a primitive
I thought that chunking was another such fundamental primitive. I thought: would it be possible to invent a simple differentiable building block that encapsulated the idea of chunking? Based on my experience with language modeling, and my overall priors about the world, I felt like this would be an incredibly powerful module that would allow models to organize raw data into more meaningful units. Surely this was a more appropriate way of modeling language and much more!
Tokenization as a case study
Back then, I had already formulated tokenization as a major problem that I wanted to solve. The first reason is, as I explained in my previous blog, an appeal to aesthetics and generality, which to me felt important enough. But the more specific reason was that I felt that the proper way to solve tokenization would be through creating a differentiable chunking mechanism, which would be so much more powerful. It could be used on any data, and recursed to develop a hierarchy of abstractions. This is still the way that I like to pitch the problem now, as some researchers that have talked to me directly might know from the way I hinted at the H-Net project over the last few months.
Overcoming tokenization is not about tokenizers, but about learning abstractions. Discovering a tool that can do this will unlock new capabilities.
Stuck.
At this point, tokenization and chunking became one of my personal “holy grail” problems. But how can one create such a differentiable chunking primitive? Grouping discrete units of data together is, of course, a discrete selection problem, which is generally very hard for differentiable optimization. Unfortunately, I had absolutely no idea how to do this. So this was always just an idle thought in the back of my head, and I never actively worked on it.
Information-based Chunking
In 2024, I started idly thinking about this again; maybe partly motivated by Cartesia’s focus on audio, where it seemed like differentiable chunking could be very useful.
Total information content as a chunking strategy
I finally had an idea for how to do this: I still didn’t know how to make this process differentiable, but at the very least, perhaps we could come up with some smart general principles for what chunks should look like. It seemed like the key for a chunk to be “meaningful” is that it should have a certain amount of “information” in it. And there’s an easy proxy to create such constant-information chunks: Simply train a neural network to model the information content of the data (which can be read off of the conditional distributions of a standard autoregressive model, of course) and use that to segment the data, by grouping tokens together until the total negative log-likelihood of that chunk overflowed some threshold. This intuitively had a number of desirable properties, such as
- if there were a lot of low-information tokens that are very easy to predict, then there probably isn’t valuable meaning to them, so they should all be grouped together;
- if the model is surprised by the next token (such as the beginning of a word, which generally has higher entropy and intrinsic information), then the model would be forced to draw a boundary and start the next chunk, which ideally represented a new unit of meaning.
(Fast-forwarding a bit: in H-Net, we don’t completely understand where and why it decides to draw chunk boundaries, but we did notice a connection to this uncertainty principle; it tends to draw boundaries when surprised. But that’s the subject for a future post.)
The project begins
About a year ago, in summer 2024, I gave a research talk (an early version of my [Tradeoffs blog post]) to my academic lab at CMU and highlighted some key problems and approaches that I thought could be important. Solving tokenization and finding a way to create hierarchical models that fit the natural information of the data was one such problem, and I pitched the above approach as a concrete direction to get started.
Some students got interested and started thinking about this. I was still very, very interested in the above approach about information-based chunking; Ricardo Buitrago explored it a little bit but didn’t get too far as he started working on another project on length generalization in recurrent models
Differentiable Selection with Modern Techniques
Fortunately, Sukjun refused to listen to me because he had a much better idea! (A recurring theme in this project…)
He wanted to try something loosely inspired by mixture-of-experts (MoE), the idea being that MoE (where each token gets “routed” to a fixed set of $k$ “experts”) is essentially a discrete selection problem like the one we want to solve.
The main advantage of this approach is that it provides some hope for building a differentiable chunking mechanism in an end-to-end model, unlike my information-based heuristic which would require training a separate proxy model first. At the time, I actually basically didn’t know anything at all about how MoE worked, so I left Sukjun to his own devices for a long time, and he got the main ideas working relatively quickly. But there were a lot of really confusing training behaviors and instabilities, so he spent a long time building intuition and slowly improving the model.
Incidentally, it’s kind of interesting to me how obvious in hindsight, but not in foresight, the main idea is. As this project developed, and I told a bunch of people about it, their reaction usually went from “this differentiable selection problem seems impossible” to “oh yeah that might work” as soon as I mentioned the connection to MoE being another variant of a discrete-selection problem. (But as we’ll see, it’s much harder than just straight up applying MoE!)
Discovering Prior and Concurrent Works
When we started this project, we hadn’t done a very serious literature search attempt because there are incredibly few papers on this topic – I guess it’s a pretty hard problem after all. Over the course of the project, we discovered two related works that were most directly related, and I expect we’ll get plenty of questions about how they compare.
Hourglass and Dynamic Pooling Transformer
Around late October 2024, we discovered the Dynamic Pooling Transformer (DPT)
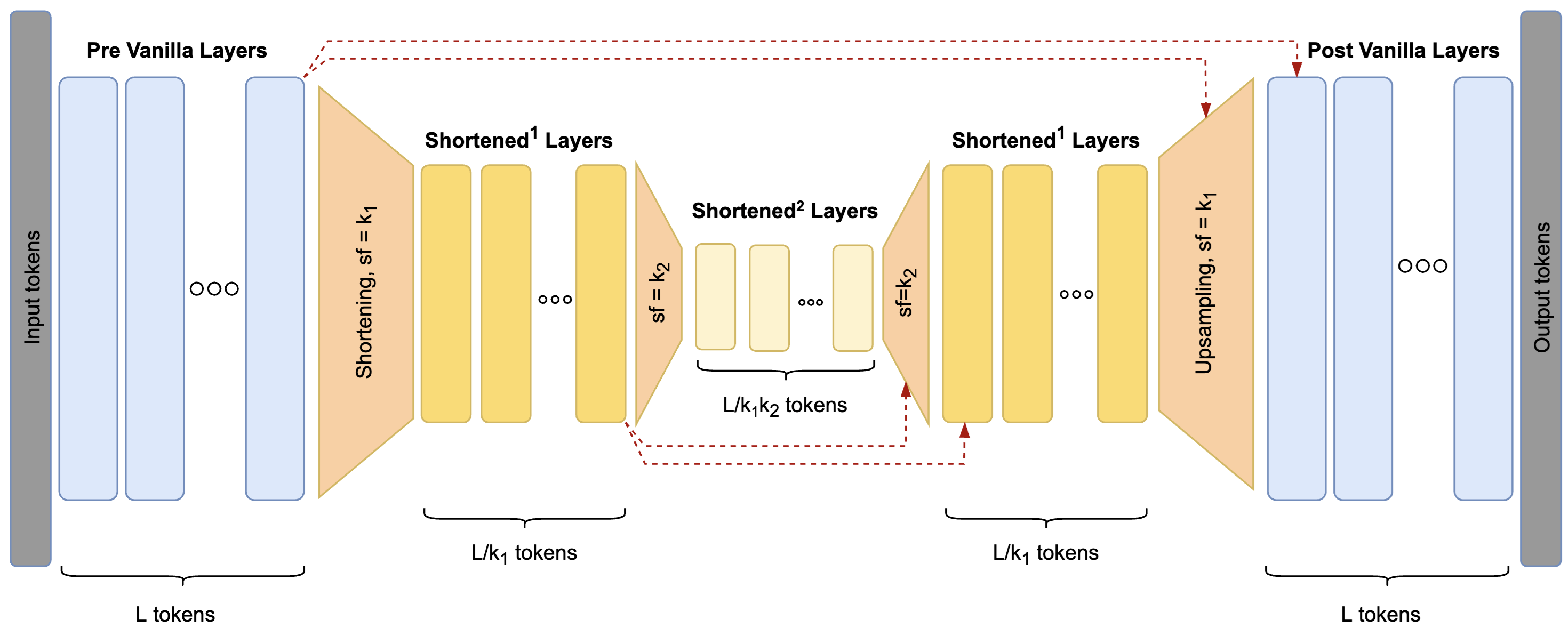
Their motivation for how to overcome the discrete-choice problem was delegating to stochastic reparametrization techniques, namely the Gumbel-softmax trick
Actually, before we found this paper we had tried many variations of Gumbel noise already; I’m rather fond of the Gumbel-softmax trick myself and kept trying to get Sukjun to incorporate it. But it never seemed to help empirically 🥲
A missed naming opportunity
Just for fun, I’ll mention an earlier working name for the model I considered.
I think Hourglass is an aesthetically pleasing name, and also elegantly describes the characteristic shape of the architecture; it’s essentially equivalent to a U-Net, but refers to the actual tensor shapes (gradually shrinking and then expanding the sequence, like an hourglass figure) instead of the abstract downsampling/upsampling flowchart.
I thought about calling our model the Hourglass Network (shortened to H-Net), and the inner dynamic chunking module the TickTok layer. I really liked this name because there are several layers of meaning to it:
- Hourglass still refers to the shape of the hierarchical network. (Calling it “Network” also differentiates it from the Hourglass Transformer, I suppose, since one of our important details was using SSMs in the outer layers.)
- The network structure could be viewed as multi-rate sequence modeling involving modalities or streams of data that tick at different rates, such as characters vs. words, or audio vs. phonemes. The TickTok layer would be the interface between these modalities.
- The network could also be viewed as performing a form of dynamic tokenization that compresses contiguous inputs just as tokenizers do. The TickTok layer would again be the mechanism that performs this compression. (Dynamic tokenization, instead of dynamic chunking, was also the working name for this project for a long time.)
- Finally, there’s a time-related theme to all of it: Hourglass Networks would be defined as models that have temporally-dynamic downsampling rates, where the core mechanism is the “tick tock” layer.
Unfortunately, I was a bit concerned about the name “Hourglass” being confused for parallel lineages of work; it’s also been used by plenty of other unrelated models. “TickTok” might also have been a little cheesy; and the TikTok name is also of course a well-recognized brand that might be confusing, and has also already been used by a very popular tokenizer. So we didn’t go with it. Alas 🥲
(I still liked the H-Net name, so we kept it and later “backronymed” it to Hierarchical Network. In my head I still like the name H-Net for this Hourglass connection though.)
Byte Latent Transformer (BLT)
By December, we had made a lot of progress and pretty much had the main architecture done (in particular, Sukjun had come up with the smoothing module which at the time we were calling the “EMA detokenizer”; as we show in the paper’s ablations, this was one of the most important new techniques introduced).
At this point, the Byte Latent Transformer (BLT)
A deeper dive into this approach
There is one major difference between the original idea I had and what BLT did. Since I’m not going to work on this approach, I might as well put it here.
In my idea, although I also think of it as an “entropy-based approach”, the actual quantity used to determine chunk boundaries is the information content or negative log-likelihood of the next token. In BLT, the quantity used is the conditional entropy $H(x_t | x_0, \ldots, x_{t-1})$.
The intuition in both is that segmentations should happen if the model is “surprised” by the next token, or if the current chunk has “enough information”. But surprise/information is better measured by the former quantity, not the latter! A concrete example is any conditional distribution that puts most of its mass on one vocab word $w$; this conditional distribution would have very low conditional entropy and so any entropy-based heuristic would never create a new chunk. But in the rare event that the actual next word is a different word $v \neq w$, the model should be very surprised and draw a boundary. The negative log-likelihood captures this actual information content.
I’m a little confused by why both DPT and BLT used the conditional entropy instead. Maybe I’m missing something, or for some reason empirically it just works better?
H-Net vs. BLT
We expected to get a lot of questions about BLT since it’s currently the most well-known tokenizer-free method; and indeed after releasing H-Net we have already gotten a lot of questions about the comparison. So I decided to add this note just to have a place to point to for those asking for a direct comparison, although it’s out of the way of the main story. I’ll be pretty explicit here – but very happy to be corrected by the authors (or anyone else) if I say anything incorrect!
tl;dr
- BLT is not actually end-to-end
- H-Net should both be easier to use and perform better than BLT
We can roughly factor the overall design of this family of hierarchical models into two parts: (1) the chunking strategy (2) the architecture.
Chunking
The chunking strategy is the core, and is the focus of both of these papers. The main advantage of H-Net is that it’s actually end-to-end, able to learn the chunking strategy together with the model.
Additionally, the entropy-based approach of BLT has some intrinsic weaknesses:
- It requires significant extra work (to train an auxiliary conditional entropy model).
- It can’t be nested into deeper hierarchies, which was one of the core motivations of H-Net and we showed significantly improved performance: in all our experiments, we found H-Net (2-stage) > H-Net (1-stage).
In the H-Net paper, we used SpaceByte
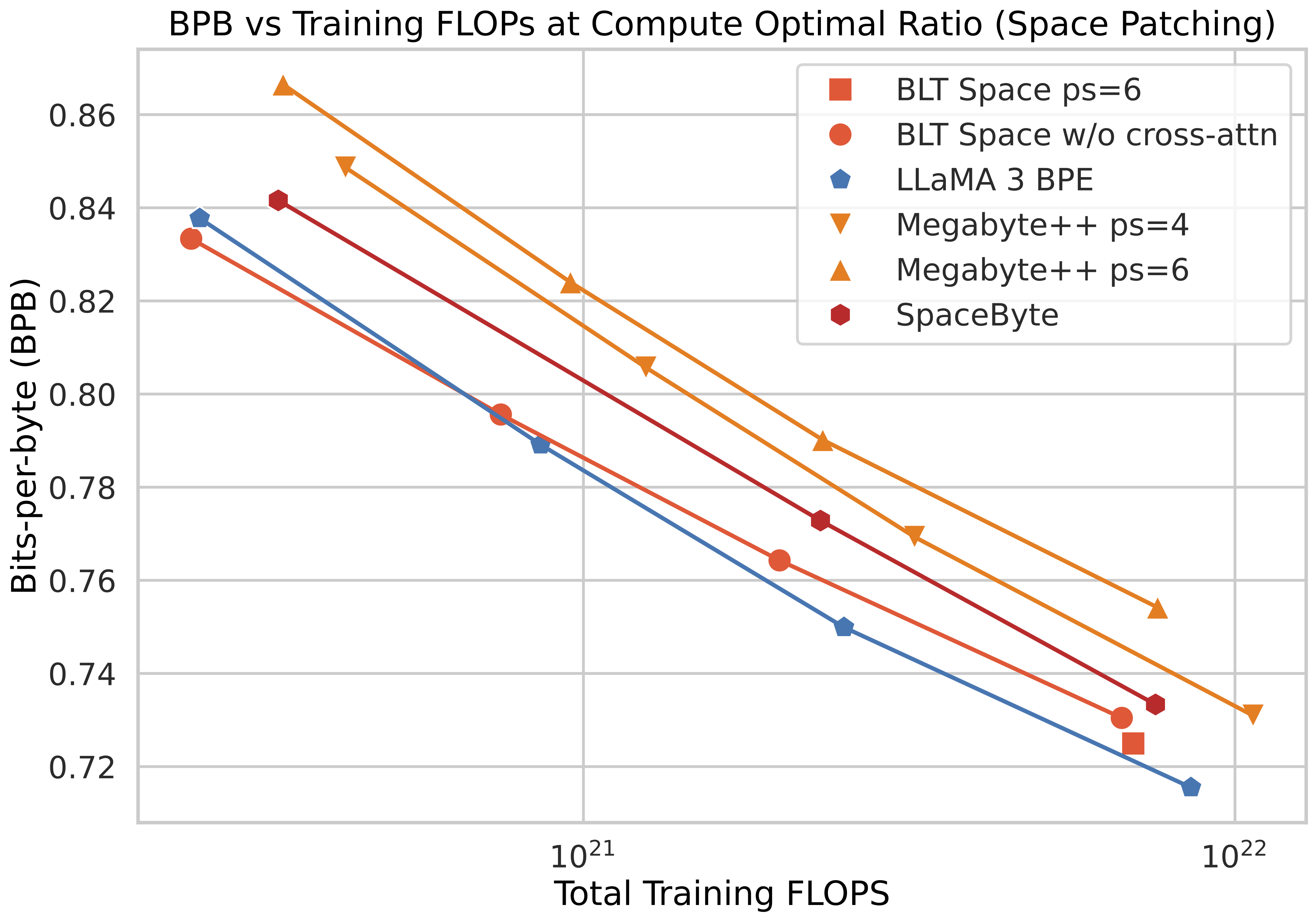
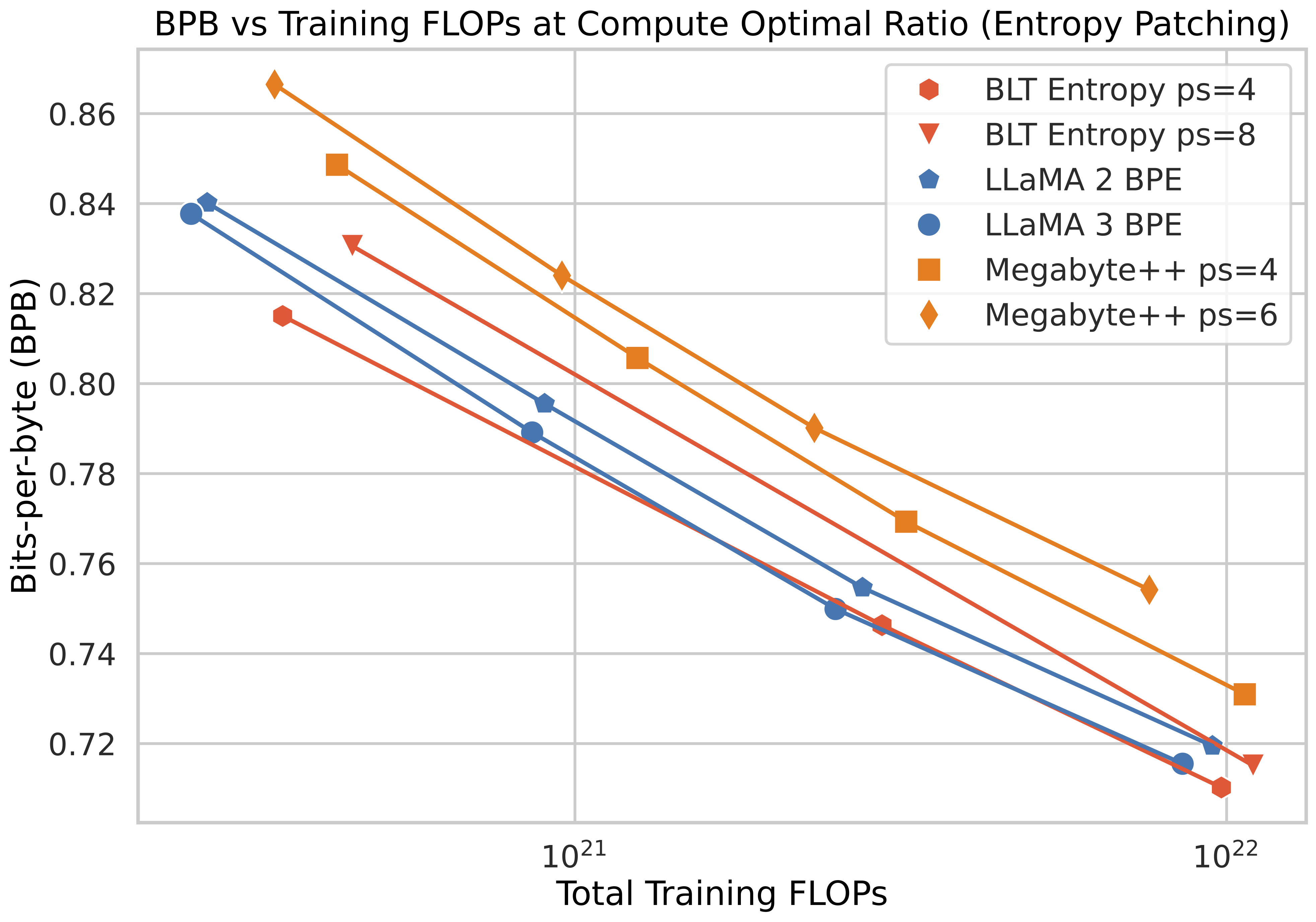
Note that the advantage of BLT over SpaceByte is that the entropy strategy is more flexible: it can be applied to languages without delimiter-based segmentation strategies, or potentially even non-discrete sequences of data. However, it’s still strictly less flexible than the dynamic chunking (DC) mechanism of H-Net. The only advantage I can think of for entropy/information-based chunking is that perhaps it could be easier to prove certain flavors of theory for tokenization
Architecture
The architectural components of the models are generally orthogonal to the chunking strategy. BLT introduced a number of unique components, such as a new type of chunk-aware cross-attention layer, and large tables of “hash n-gram embeddings”. We think both of these are not necessary; H-Net works just fine without these additional techniques, although I believe that they could also be incorporated into H-Net if desired.
So overall, we felt that the full BLT model is an overly complicated baseline to set up and compare against, and (as explained in the paper) we used SpaceByte as a representative example of BLT-like models. But I still like the idea of BLT and I’m glad it’s published!
A World of Improvements
I think the architecture has been relatively stable since early 2025, but we spent a long time trying to understand and simplify every part of it. For example (this is just a small subset),
- Architecture components: our final architecture included post-norm layers at the end of every sub-network, as well as linear projections on the residual connection. We spent a long time trying to remove these since I felt like they were non-standard techniques (most U-Nets don’t have these) that complicated the model. But in the end, they seem very useful—maybe essential—and we kept them.
- Sparsity auxiliary loss: Our auxiliary loss targets a specific down-sampling ratio. This seems a little artificial to me and introduces an annoying new hyperparameter (thankfully, the only one!). I felt like it would be cleaner to simply impose a “sparsity loss” that encouraged higher compression rates (it would be counter-balanced by the main loss function which encourages more compute, hence lower compression rates). We found some things that sort of worked but it didn’t seem as consistent, so for this version of the H-Net we kept the targeted “ratio loss”.
- Chunking mechanisms: We tried so many different variations of the routing module, upsampling step, downsampling step, smoothing module, and every other component. Sukjun’s PowerPoint deck of ideas and variations has hundreds of slides, and we were only able to report a very small subset of ablations in the paper of things we did.
- Layer allocation: Normal LLM scaling laws might be concerned with how to scale the width and depth of the model as the parameter count grows. But here, there are so many more choices for how many layers to put in each sub-network and how wide to make them and so on. Beyond that, the question of which layers to use (e.g. Transformer vs. Mamba) in each network is also not obvious, and required tons of experiments to understand (and I’m still not sure we have a completely clear grasp of how they predictably affect performance).
Although our final (current) design has a lot of moving parts, they all had concrete motivations, and are as simple as we could make it without sacrificing stability or performance.
This particular abomination was mine, which didn't work of course 😂
I haven’t been able to run experiments personally in a while, and it was like watching an artist at work to see Sukjun improve the architecture steadily over time with multiple creative and essential ideas. I have to say that this was one of the most difficult empirical projects I’ve witnessed (and I think I’m somewhat decent at creating architectures 👀). Normally when tuning models, one hopes that different axes of variation act somewhat independently so they can be ablated in isolation and we can perform a “coordinate descent in design space”. But somehow for this architecture, it felt like there were 12 different axes that were all critical and that all had to interact together in exactly the right way. There were so many times when we thought that option “A” was better than “B”, before changing some other design decisions and flip-flopping to B, before changing even more things and going back to A. And this happened with every axis of variation. Even after we had all the main ingredients, it was really difficult to get them to interact together seamlessly. But eventually it all came together, thanks to Sukjun’s intuition and persistence.
Tradeoffs of SSMs and Transformers
In my previous blog post, I argued that we as a community should care about getting rid of tokenization. I hope the H-Net has done that, or at least shown the first step that it’s possible. Aside from that, there are a couple of points in the previous post that I’ll specifically call back to.
Noisy data
I proposed [a hypothetical litmus test] involving sequences padded with information-less noise tokens. This was a thought experiment that partially motivated why I was so interested in hierarchical models. The idea is that one should be able to train some lightweight encoder and decoder networks that perform the compression of each chunk, folding each contiguous run of noise tokens into the previous meaningful token. This should be able to compress and strip away the noise tokens before feeding it to a main network that operates just over the meaningful tokens.
Can the H-Net actually solve this in practice? I don’t know, maybe some more work would need to be done. I was more interested in the litmus test as a thought experiment to guide architecture design, not necessarily as an actual synthetic task.
SSMs as compressive models
Finally, let me show perhaps my favorite experiment from the paper, even though this is buried somewhere late in the ablations because it’s subtle.
In the previous post, I asked the question: [Is compression a bug, or a feature?] And I floated the idea that perhaps SSMs had hidden strengths due to their compressive abilities.
The more obvious piece of evidence I gave for this was comparing the inductive bias of SSMs and Transformers, for example, by contrasting these two facts:
- Transformers and SSMs have similar performance on tokenized language (with caveats)
- Transformers seriously underperform SSMs on untokenized language
My intuitive explanation was that on high-resolution data without meaning (such as characters), attention is a poor inductive bias, and understanding the data requires compressing it. Ablations in the H-Net paper corroborate this: any parts of the model interacting directly with byte-level resolution strongly benefit from SSM layers.
This raises a natural question though: is the importance of Mamba layers because
- they are simply better at processing fine-grained byte inputs, as we already knew?
- or because they are better for compressing information into the next stage, even if given coarser inputs?
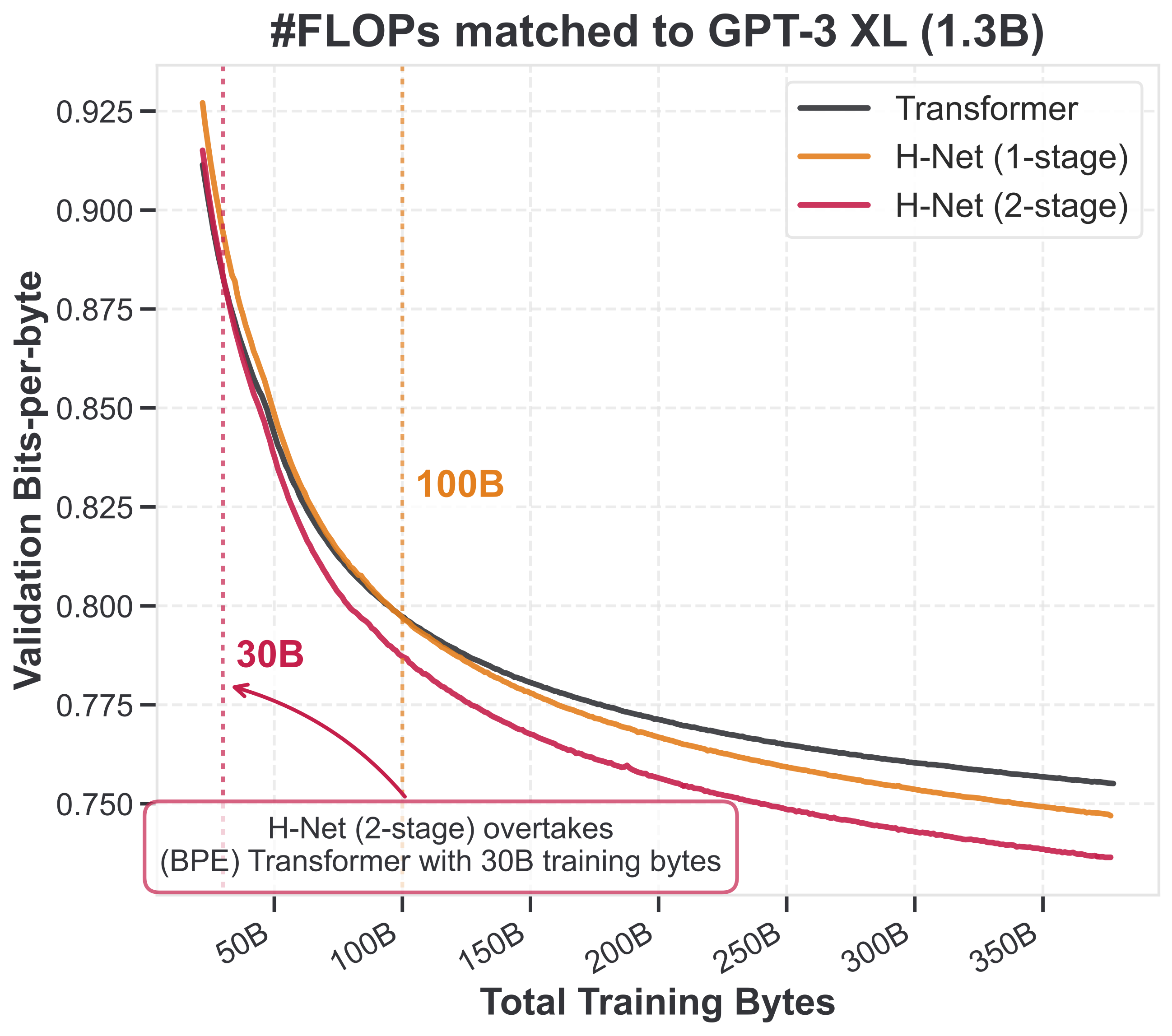
We can disentangle these two hypotheses by simply applying an H-Net on data that’s not byte-level. After all, it’s just a generic sequence model architecture that can be applied on any data! In particular, let’s apply it to data that’s already BPE-tokenized.
- If the first hypothesis holds, then we would expect Mamba to not help in the encoder/decoder, since (as mentioned above) it has similar performance to Transformers on standard tokenized language modeling.
- If the second hypothesis holds, then we would expect that encoders/decoders using some Mamba layers to be better than pure Transformer layers.
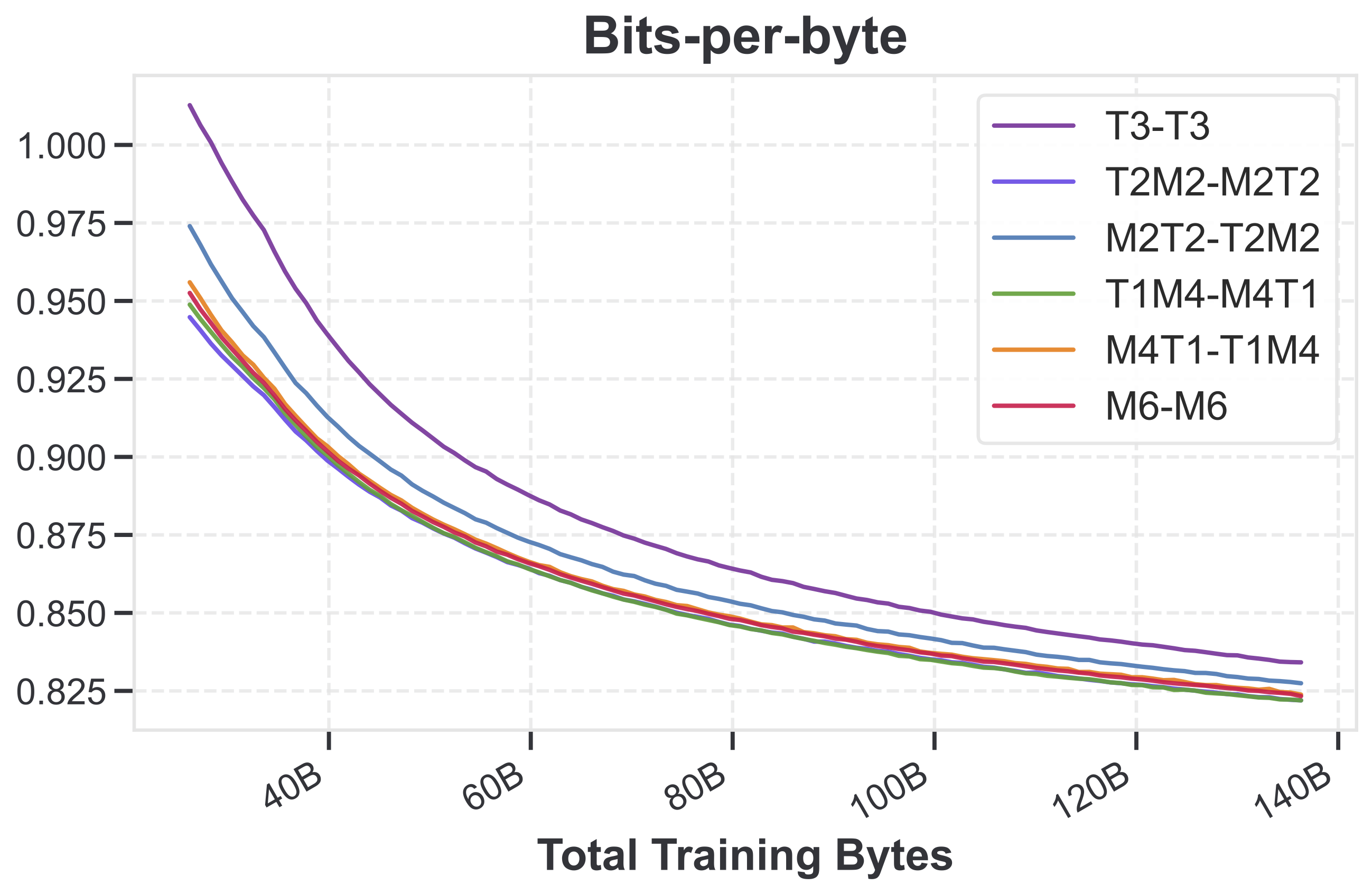
This figure shows that it’s indeed the second hypothesis that holds. This is really interesting and to me provides serious evidence that SSMs really are doing something interesting that other models can’t do, and that perhaps compression is fundamental to intelligence.
The Future
There’s a ton of stuff we could do and ideas that we have that we left on the table. A bunch of questions are pointed out in the Discussions section of the paper, and in my next post, although this is only a subset of the wide range of follow-up directions that I think will be interesting to work on.
One question that I expect we’ll get is: do H-Nets actually scale better? In the paper, we showed training loss curves, where they display a striking trend of seeming to scale better with data. We use these as proxies for a qualitative assessment of their performance, which I do believe is valuable (a justification is in the Discussion section of the paper). For various reasons I also actually believe that H-Nets will shift the scaling law curve in a non-trivial way (still considering writing a follow-up blog post about this…). However, what we did aren’t formal scaling laws.
Why didn’t we do those? Well, I guess the main reason is limited compute and more so the sheer difficulty of developing this model, which is where all our resources were invested. At no point did it seem worth completely freezing the architecture to run out expensive formal scaling laws, when I think we were able to get an intuitive understanding of its behavior from our proxy protocol; and moreover, when it always seems like there are core questions we don’t understand and low-hanging improvements to make to the model.
We didn't because we only ran things out enough to follow our protocols and provide signal to improving the model.
We have a lot of ideas for where to go from here; I’ll touch on some of these in the next post.