Hydra Part II - The Model

- Part I - Matrix Mixer Framework
- Part II - Hydra: The Model
In our previous post, we systematically compared various sequence models with different mixer matrices, and the quasiseparable SAM mixer emerged as the top performer. So, what exactly is it?
Recap: SSMs Are Semiseparable Matrix Mixers
Before diving into the details of quasiseparable SAM mixers, let’s briefly revisit some key findings from Mamba-2
Defintion of Semiseparable Matrices
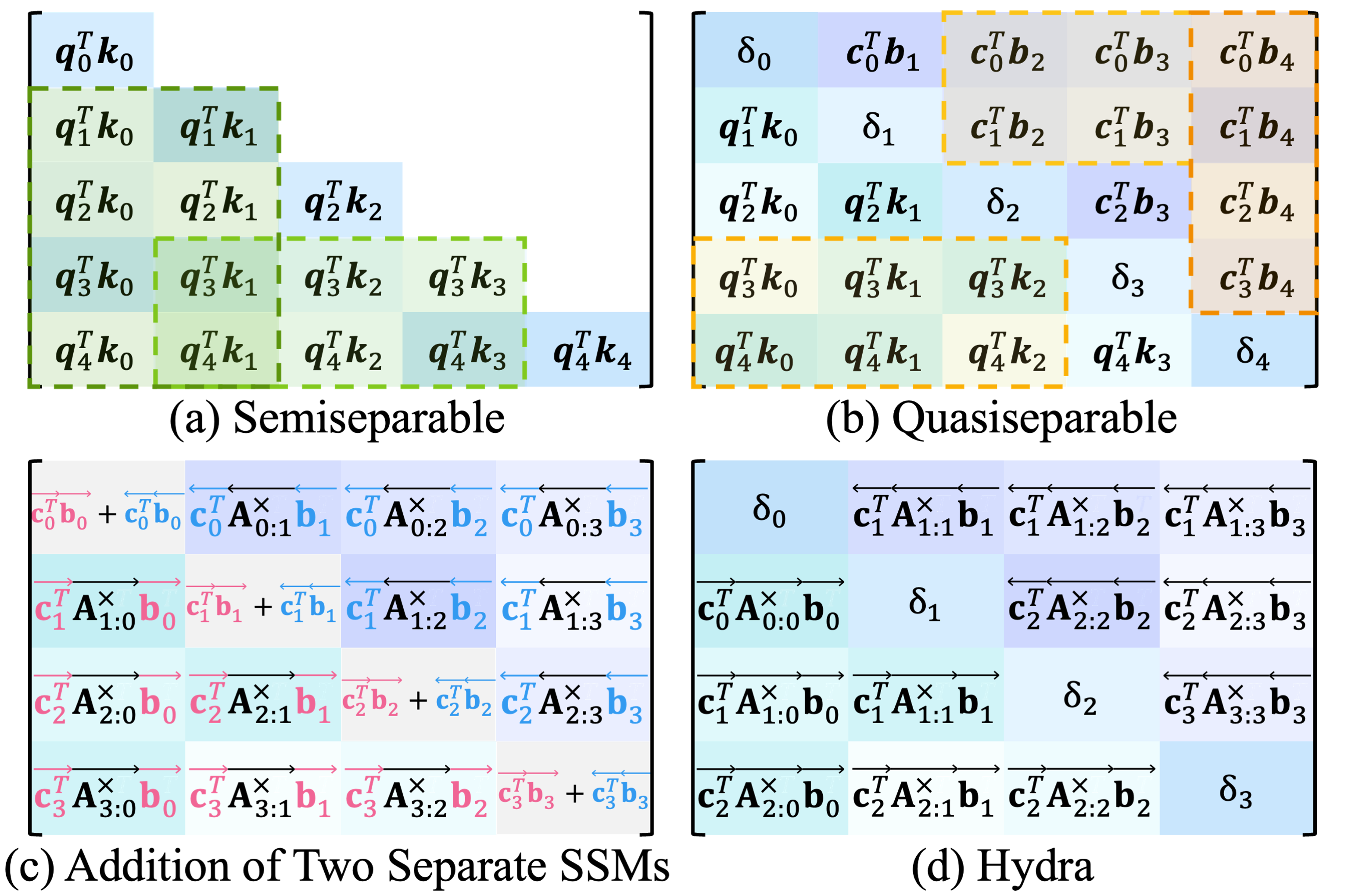
A lower triangular matrix $\textbf{M}$ is $N$-semiseparable iff any submatrix from the lower triangle (on or below the diagonal) has a rank of at most $N$. See (a) in the figure below.
So why are SSMs semiseparable matrix mixers? Using our previously defined matrix mixer framework, we can represent SSMs as follows:
\[\begin{align} \textbf{y}_t &= \sum^{t}_{s=0} \textbf{C}^T_t \left(\prod_{k=s+1}^{i} \textbf{A}_{k}\right) \textbf{B}_s \textbf{x}_s \\ \\ \textbf{Y} &= \text{SSM}(\textbf{A}, \textbf{B}, \textbf{C})(\textbf{X}) = \textbf{M} \textbf{X} \space ,\\ \\ m_{ij} & = \textbf{c}^T_i \textbf{A}_i \cdots \textbf{A}_{j+1} \textbf{b}_j \end{align}\]where each matrix $\textbf{A}_i \in \mathbb{R}^{N \times N}$ and vector $\textbf{c}_i, \textbf{b}_i \in \mathbb{R}^{N \times 1}$. This decomposition shows that SSMs are indeed semiseparable mixers. [If you are not familiar with this concept, we recommend checking out this blog post for a great explanation.]
Semiseparable matrices are an excellent choice for mixer matrices – they are sub-quadratic, performant, and can be extended to handle sequences of various lengths. However, there’s one significant limitation: due to their definition, the upper right triangle of semiseparable matrices is filled with zeros, making them inevitably causal. This limitation makes SSMs incapable of bidirectional sequence processing.
Why is bidirectionality important? Bidirectional processing is crucial for several reasons. One major reason is its importance in handling multiple modalities, such as processing 2D images. Without bidirectionality, models can’t fully leverage information from both past and future contexts within a sequence, which is essential for comprehensive data analysis across various applications.
A straightforward way to make SSMs bidirectional is to use two separate SSMs: one for forward sequence processing and one for reverse sequence processing. There are several approaches to combine their outputs, such as adding, multiplying, or concatenating them
But what if we could use the matrix mixer framework to systematically derive the optimal $\textbf{M}$? Absolutely, we can! In addition to the three desiderata we discussed previously – sub-quadratic complexity, extendability, and high-performance – let’s add one more requirement: bidirectionality. For the mixer matrix to achieve bidirectionality, it must feature upper triangular components. So, how should we fill them?
Structured Matrix of Our Choice: Quasiseparable Matrices
For our bidirectional sequence mixer, we choose quasiseparable matrices. So, what makes quasiseparable matrices stand out? Let’s start by looking at their definition.
Defintion of Quasiseparable Matrices by the Rank Characterization.
A matrix $\textbf{M}$ is $N$-quasiseparable iff any submatrix from either the strictly upper or lower triangle (off from the diagonal) has a rank of at most $N$. See (b) in the figure above.
At first glance, this definition might seem similar to that of semiseparable matrices. To clarify, let’s highlight the key differences between quasiseparable and semiseparable matrices:
| Semiseparable | Quasiseparable | |
|---|---|---|
| (I) | any submatrix from the lower triangle | any submatrix from either the strictly upper or lower triangle |
| (II) | on or below the diagonal | off from the diagonal |
Quasiseparable Matrices $\supset$ Semiseparable and Low-Rank Matrices
Although the differences between quasiseparable and semiseparable matrices might seem subtle, they lead to significant improvements in expressivity. According to difference (I), semiseparable matrices zero out the upper triangular elements, while quasiseparable matrices extend to include these elements, enabling bidirectionality. Consequently, semiseparable matrices can only generalize mixers that use causal low-rank matrices, such as Linear Attention, whereas quasiseparable matrices generalize typical low-rank matrices. Moreover, both differences (I) and (II) mean that quasiseparable matrices not only generalize but also extend semiseparable matrices.
- Quasiseparable matrices generalize low-rank matrices.
- Quasiseparable matrices generalize and extend semiseparable matrices.
Quasiseparable Matrices $\supset$ Two Separate SSMs
We now understand that for bidirectional processing scenarios, quasiseparable mixers are indeed better than semiseparable matrices. But what makes quasiseparable mixers superior to the bidirectional extensions using two separate SSMs?
Heuristic variants that use the Hadamard product and concatenation
In contrast, addition-based variants
- Quasiseparable matrices are strictly more expressive than mixer matrices of addition-based bidirectional SSMs.
This property of complete freedom in the diagonals of quasiseparable matrices is more evident in another definition of quasiseparable matrices:
A matrix $\textbf{M}$ is $N$-quasiseparable if each element $m_{ij}$ satisfies:
\[\begin{equation} m_{ij} = \begin{cases} \overrightarrow{\textbf{c}^{T}_{i}} \overrightarrow{\textbf{A}_i} \cdots \overrightarrow{\textbf{A}_{j+1}} \overrightarrow{\textbf{b}_{j}}, & \text{if } i > j \\ \delta_{i}, & \text{if } i = j \\ \overleftarrow{\textbf{c}^{T}_{i}} \overleftarrow{\textbf{A}_{i}} \cdots \overleftarrow{\textbf{A}_{j-1}} \overleftarrow{\textbf{b}_{j}}, & \text{if } i < j\\ \end{cases},\\ \end{equation}\]where each $\delta_i$ is a scalar, $\textbf{b}_i, \textbf{c}_i \in \mathbb{R}^{N \times 1}$, and $\textbf{A}_i \in \mathbb{R}^{N \times N}$.
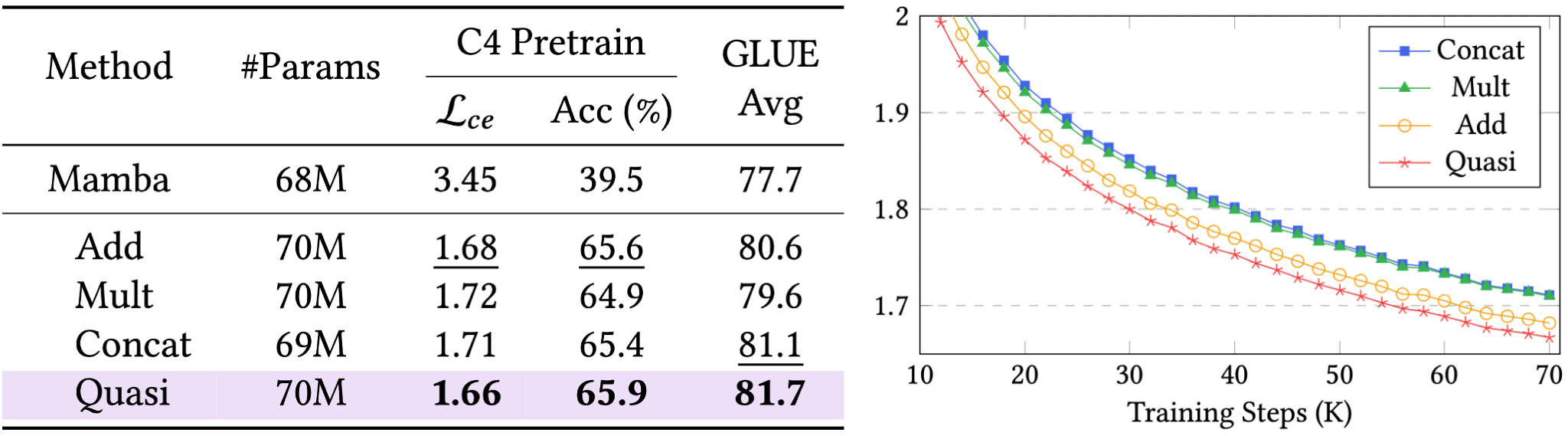
These are the actual results we obtained for the C4 and GLUE benchmark, along with the validation loss curve. Supported by these theoretical claims, our Hydra model, which uses a quasiseparable mixer matrix, indeed has shown superior performance to previous heuristic bidirectional extensions!
Hydra: Our Main Bidirectional Sequence Mixer
Implementation
Now that we’ve confirmed quasiseparable matrices as the go-to mixer matrices, we fully leverage them to propose the two-headed Mamba – Hydra. Take a look at part (d) in the figure above, which illustrates the mixer matrix of Hydra, and also notice it’s also our previosly defined SAM! Utilizing an SSM, which is a semiseparable mixer, we can implement Hydra with the following formula: \(QS(\textbf{X}) = \texttt{shift}(SS(\textbf{X})) + \texttt{flip}(\texttt{shift}(SS(\texttt{flip}(\textbf{X})))) + \textbf{DX},\) where $\textbf{X}$ is the input sequence, $\texttt{flip}(\cdot)$ denotes a function that reverses the input, $\texttt{shift}(\cdot)$ denotes a right-shift function, and $\textbf{D} = \text{diag}(\delta_1, \cdots, \delta_L)$ represents the diagonal elements of $QS$. Here, $QS(\cdot)$ and $SS(\cdot)$ are the mixer matrix of Hydra and an SSM, respectively.
Among the various iterations of SSMs, we adopt the latest one – SSD from Mamba-2. Since SSMs are sub-quadratic, this simple implementation maintains the sub-quadratic cost. Compared to heuristic extensions that use two separate SSMs for bidirectionality, Hydra shares the input processing function $f_X$ for forward and reverse sequence processing, which nearly halves the number of parameters.
You can check out the actual code. To sum up:
- Hydra’s matrix mixer is meticulously parameterized to be a quasiseparable matrix with enhanced expressivity through shift operations.
- Hydra is sub-quadratic and super easy to implement using existing SSM implementations like Mamba.
- Hydra greatly reduces parameter counts compared to bidirectional extensions using two SSMs.
Performance
We have seen that Hydra outperforms heuristic bidirectional extensions of SSMs, but how does it compare to state-of-the-art methods? Surprisingly, Hydra surpasses all previous models, including Transformer-based models such as BERT and ViT. When matched for the number of parameters, Hydra consistently shows the best performance across both NLP and Vision domains, highlighting its versatility.
| NLP | Vision | ||||
| Method | # Params | GLUE Avg | Method | # Params | Top-1 (%) |
| BERT | 110M | 83.5 | ViT-B | 87M | 78.8 |
| MLP-Mixer | 112M | 77.5 | S4-ViT-B | 89M | 79.4 |
| FNet | 112M | 75.8 | Hyena-ViT-B | 88M | 78.4 |
| M2 | 116M | 80.9 | Mamba-ViT-B | 89M | 79.1 |
| Hydra | 112M | 84.3 | Hydra-ViT-B | 91M | 81.0 |
On the GLUE benchmark, Hydra outperforms BERT by 0.8 points. On ImageNet-1K, Hydra improves by 2.2 points over ViT. These results underscore Hydra’s capability to set new standards in both natural language processing and image classification tasks!
Epilogue
Lately, the demand for large-scale computation has never been higher. Since the emergence of Mamba, interests in structured matrices has surged, and now is their time to shine. Structured matrices offer an exciting approach to efficient and powerful input processing, similar to how M2 improved over MLP-Mixer.
In recent years, we’ve seen numerous groundbreaking works showcasing promising results using structured matrices like Mamba. If the community strives together, just as we have spent about seven years investigating and improving Transformers, we believe there is enormous potential for further advancements through systematic exploration of different structured matrices, along with better optimized training settings (which have been fine-tuned for Transformers).
A big shout-out to the recent BTT