Cross-Architecture Distillation Part II - Phi-Mamba-1.5B Model and Training Laws
- Part I - MOHAWK
- Part II - Phi-Mamba
In Part I of this series, we covered important terminology, the Mamba-2 architecture, and the MOHAWK architecture. We also demonstrated Mamba-2’s ability to match the self-attention matrix of Transformers, which influenced our choice to use it as the student model for validating our MOHAWK method.
In this section, we will explore the training laws regarding each of the three stages of MOHAWK and empirically validate the importance of all stages. We use the cumulative insights gained to then distill a fully subquadratic Mamba model using only 3B tokens - less than 1% of many of the other models’ token budget - while being competitive with many of the current state-of-the-art open-source subquadratic models! We also distill a strong Mamba-Attention hybrid.
Final Results
We empirically validate the MOHAWK framework by distilling the pretrained Phi-1.5 model into a 1.5B Mamba variant, dubbed Phi-Mamba. Our final model was distilled with only 3B tokens, with a 80M/160M/2.76B token split among Stage 1/2/3, from the C4 dataset with a context length of 2048. The choices for these token splits were influenced by our verification of the importance of all three stages and training laws that determined, given a fixed token budget, how to allocate resources, which we detail in the following sections.
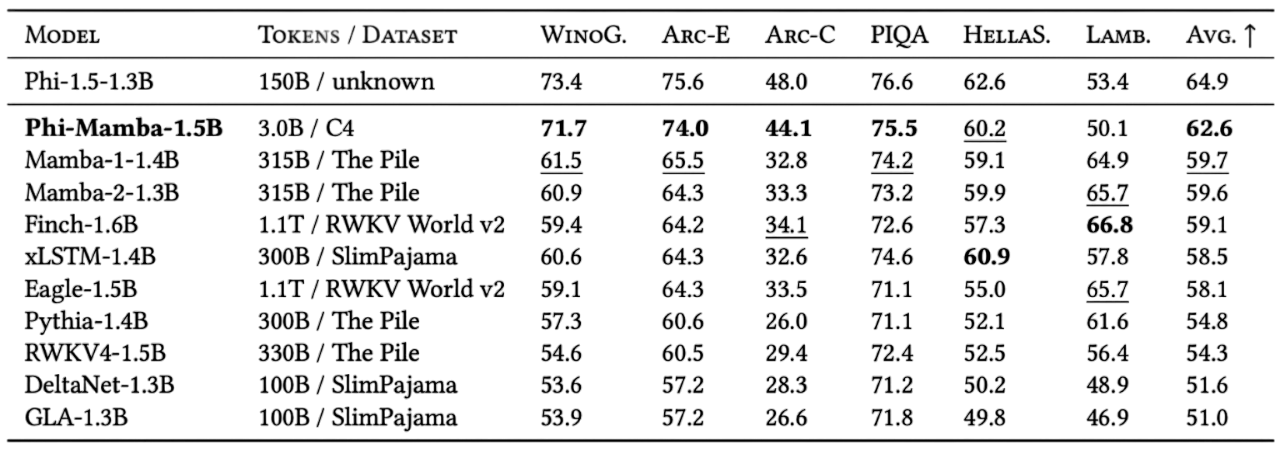
Importance of Each MOHAWK Stage
A brief recap of the three stages of MOHAWK are
1) Matrix Orientation: matches the matrix mixer of each respective block.
2) Hidden-State Alignment: independently compares the block output given the same input across all layers of the student model.
3) Weight-Transfer and Knowledge Distillation: performs knowledge distillation of logits from teacher to student and copies over crucial weights from the teacher model.
Each stage plays a crucial role as shown in our ablations below. All the runs were performed with a fixed total token count.

As expected, Stage 3’s end-to-end alignment is important as the previous stages only match the block outputs, leaving the blocks disjoint if the hidden state cannot be completely matched, as shown with both the Phi-Mamba and Hybrid-Phi-Mamba trained on Stage 3 outperform their counterparts trained with Stage 2. Of course, student models that have more mixing layers similar to the teacher may see a diminished impact of Stage 3 as the layers may be aligned more with only Stage 2.
The addition of a Stage 2 initialization provides additional synergy, boosting performance significantly compared to Stage 3 only. We also note that the effects of adding Stage 2 is more pronounced in cases where the student architecture is less similar to the teacher architecture, e.g., the improvement for Phi-Mamba which has zero attention layers is larger than Hybrid-Phi-Mamba which has four.
Stage 1 also provides a good in downstream performance. For example, only with the addition of Stage 1 on top of Stage 2 and 3 can a Phi-to-Phi distillation recover the original teacher Phi’s overall performance. And, we see in the two other architectures that performance gains can also be observed.
Training Laws for MOHAWK
We aimed to evaluate the impact the preceding stage had on the current stage’s performance.
For the Stage 2 + 3 pair, we trained Phi-Mamba instances from scratch using Stage 2 to various checkpoints. These checkpoints were then used to initialize Phi-Mamba instances that were trained using Stage 3 to different total budgets. The figure below shows that given an adequate training budget, student models initialized from Stage 2 outperform students trained only with Stage 3.
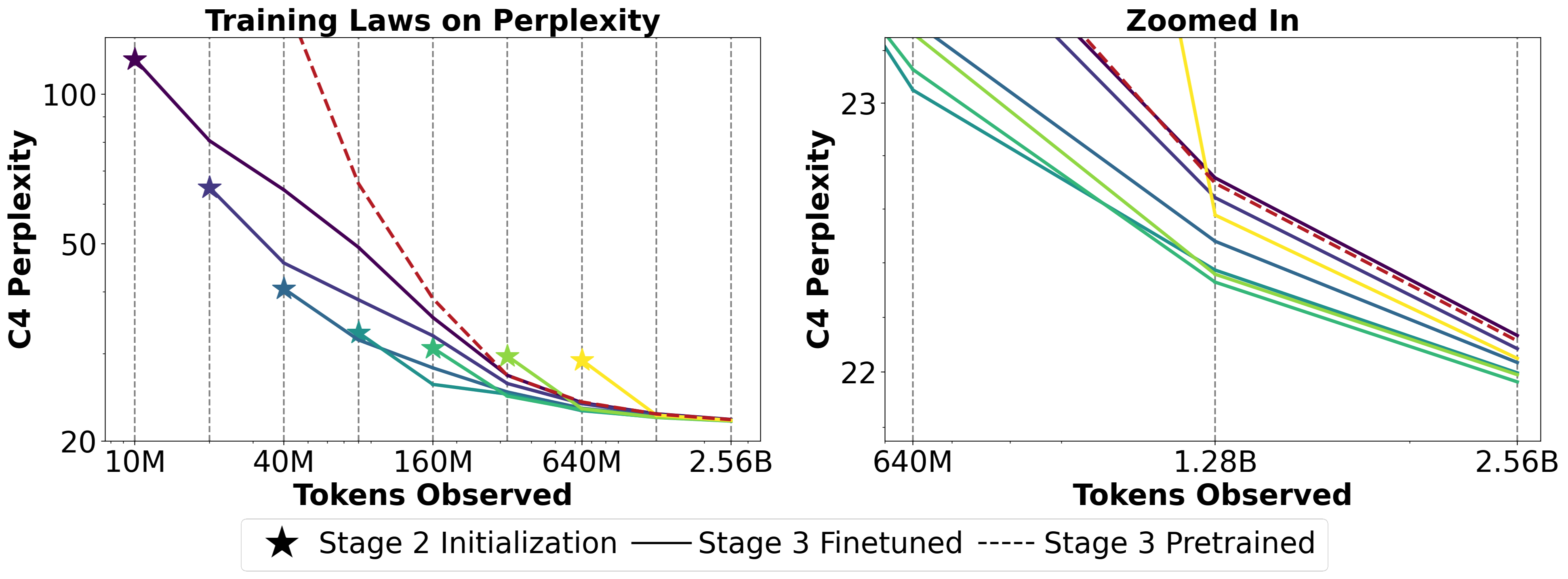
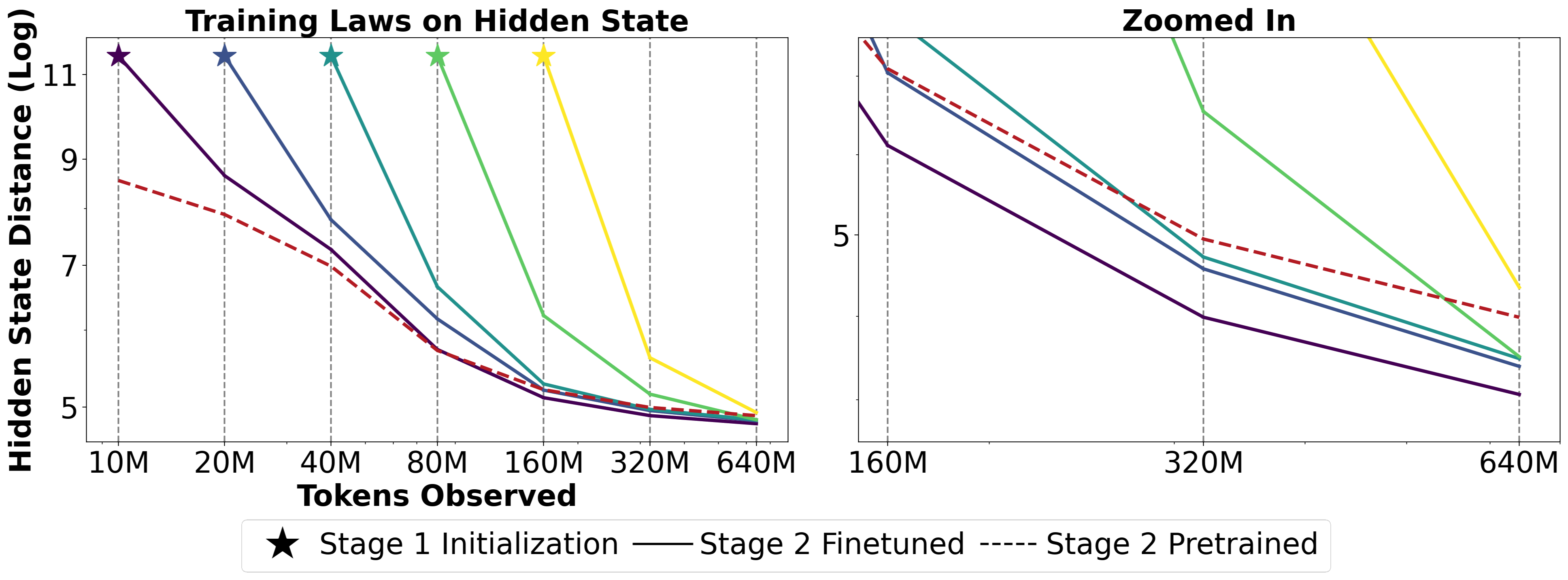
Given the previous finding, we then analyze how matrix mixer matching (Stage 1) can impact the student’s ability to match the overall mixer block with the teacher (Stage 2). Similar to before, we train numerous Phi-Mamba models using Stage 1 and use them as initializations for Stage 2 and compare them against each other and also a Stage 2 only model. Here, we find that even a small budget allocated to Stage 1 can help the subsequent stage perform better than random initialization.
Training the Final Phi-Mamba Model
Using the insights gained in the training laws above, we finalized our training regime given a fixed budget of 3B tokens. Stage 1 was allocated 80M due to the strong performance on matrix distance and hidden state distance. Stage 2 was trained for 160M tokens given the seeming saturation of both hidden state distance and perplexity when compared to the other initialization states, e.g., 10M, 20M, 40M, etc. We train Stage 3 to reach 3B tokens in total, but reduced the learning rate of the last stage to alleviate training instabilities. We hypothesize that this is due to the Stage 1 + 2 initialization’s Mamba component being quite similar to that of the teacher model, so a large learning rate coupled with disconnect between blocks, which are addressed in Stage 3, can cause training instabilities.
Hybrid Phi-Mamba Model
There has been a growing body of work that combines both Attention and SSM mechanisms, leading to improved performance over either one used by itself
Thus, we distill the Phi-1.5 model into a Mamba-Attention hybrid model that maintains only four quadratic Attention layers. The remaining layers use the Mamba-2 layer variant also used in our Phi-Mamba model. Trained with 5B tokens using the MOHAWK method, our model achieves an average score of $66.0$ on downstream metrics, outperforming Phi-Mamba’s $65.1$ and approaching Phi-1.5’s $67.2$.

Our Hybrid-Phi-Mamba model is performs comparably to strong Attention-Mamba hybrids at the 1.5B range while using less Attention layers than Samba (12) and Mamba-SWA-MLP (18). We find that interleaving the Attention layers with the Mamba layers resulted in the strongest model, an observation that was also seen in