Cross-Architecture Distillation Part I - The MOHAWK Framework

Part I - MOHAWK
Part II - Phi-Mamba

Preliminaries

We start off by summarizing some important aspects from , specifically the sequence transformation/mixer viewpoint and the Mamba-2 SSM variant.

Definition: A sequence transformation/mixer refers to a parameterized map on sequences $Y = f_{\theta}(X)$ where $X, Y \in \mathbb{R}^{(T, P)}$ and $\theta$ is an arbitrary collection of parameters. $T$ represents the sequence or time axis; subscripts index into the first dimension, e.g. $X_t, Y_t \in \mathbb{R}^P$.

In layman’s terms, sequence mixers aggregate tokens across various time steps. This ability to learn temporal interactions and information forms the foundation of modern deep sequence models, like Transformers.

Definition: Matrix mixers are a specific type of sequence mixers that can be represented as $Y = MX$ for matrix $M \in \mathbb{R}^{(T,T)}$.

Examples of matrix mixers which fall under this definition include vanilla self-attention, where $M = \text{Softmax}(\mathbf{Q}\mathbf{K}^\top)$ , linear attention , and Toeplitz matrices .

Mamba-2

Mamba-2 is a recent variant of Structured State Space Models (SSMs) which can be viewed as a matrix mixer that can be applied onto an input sequence in subquadratic time due to structured matrix multiplication. Mamba-2 is a time-varying SSM, defined as

\[\begin{aligned} h_{t+1} &= A_t h_t + B_t x_t \\ y_t &= C_t h_t \end{aligned}\]

where $B_t$ and $C_t$, like in Mamba-1 , are input-dependent projections, but $A_t$ is the identity matrix $I$ multiplied by a scalar $\alpha_t$. Importantly, Mamba-2 identified the Structured State Space Duality (SSD) connection which found that specific variants of SSMs can be viewed as a form of causal linear attention .

Formally, the Mamba-2 SSD matrix mixer can be represented as

\[\begin{equation} \label{eq:ssd-matrix-mixer} \begin{aligned} \begin{bmatrix} \alpha_{1} & 0 & 0 & \cdots & 0 \\ \alpha_{2:1} & \alpha_{2} & 0 & \cdots & 0 \\ \alpha_{3:1} & \alpha_{3:2} & \alpha_{3} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \alpha_{n:1} & \alpha_{n:2} & \alpha_{n:3} & \cdots & \alpha_{n} \end{bmatrix} \circ (C \cdot B^\top) \cdot X \end{aligned} \end{equation}\]

where $\alpha_{t:i} = \alpha_{t-1} \cdot \alpha_{t-2} \cdots \alpha_{i}$.

From this representation, one can see that Mamba-2 can be viewed as causal linear attention with a learnable causal mask!

MOHAWK Method

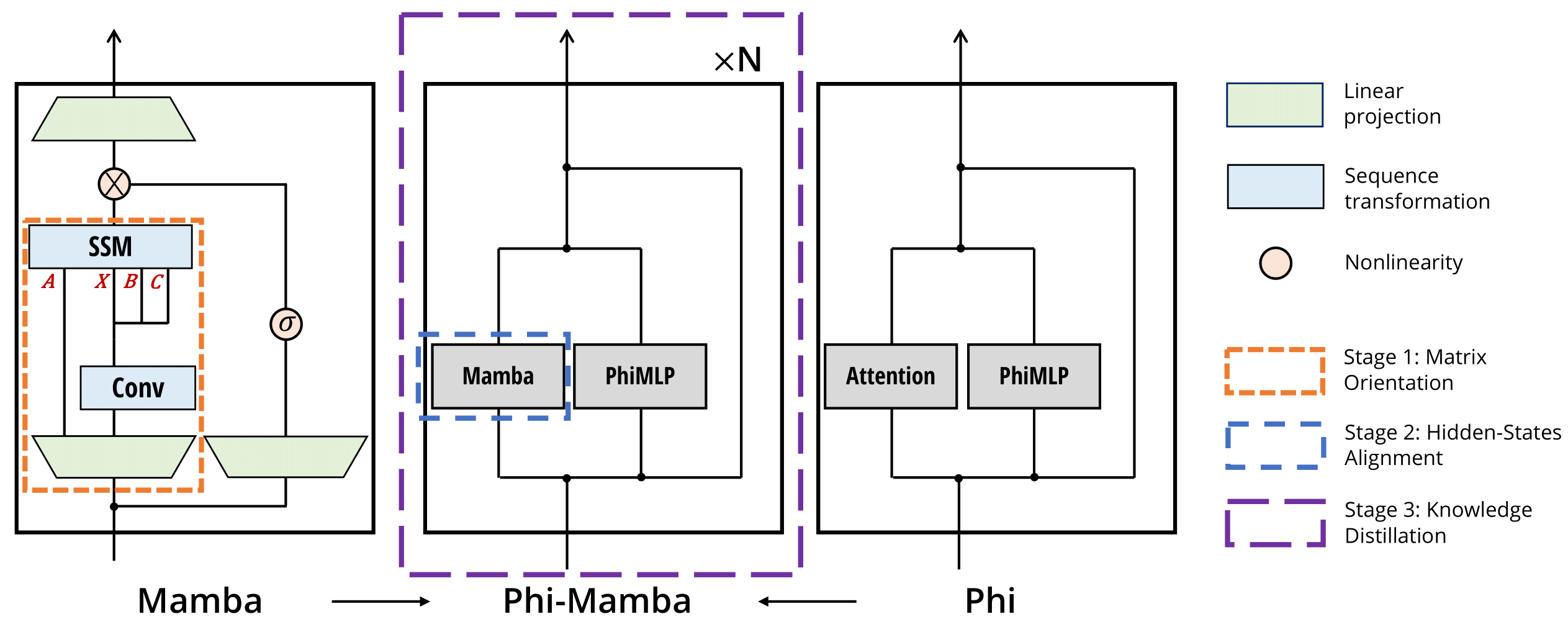
Inspired by the matrix mixer viewpoint which provides a common lense for viewing the key components of various architectures, we introduce the MOHAWK framework for cross-architectural distillation, which is composed of three stages:

Matrix Orientation
Hidden-State Alignment
Weight-Transfer and Knowledge Distillation

These three sequential stages distill the student model from the bottom up, steadily increasing the number of components distilled into at each stage until the end student model has been distilled end-to-end. We find that this multi-stage process is much more effective than traditional knowledge distillation.

Unlike traditional distillation techniques, the student model retains the overall architecture of the teacher model, differing only in the replacement of the attention matrix mixer with a subquadratic alternative. We will progressively unveil our architecture, Phi-Mamba –based on the Phi-1.5 model – along with the specifics of its distillation process.

For clarity, we refer to the term block as a repeating component that forms the backbone of the end-to-end model. Blocks are composed of layers, for instance the Llama block is composed of a self-attention layer followed by a MLP layer. Layers can be composed of numerous subcomponents, like the self-attention layer, which encompasses the projections and the self-attention mechanism, and the Mamba layer, which includes the projections, convolution, and SSM mixer, etc.

Stage 1: Matrix Orientation

We begin the first stage of MOHAWK by matching the matrix mixer of both the student and teacher. Prior to directly aligning the matrix mixers themselves, we first adjust the matrix mixer layer to be analogous to that of the teacher’s, i.e., structurally both layers are the same except the matrix mixer component. We then minimize the distance between the matrix mixer of the teacher and student layers, which can be expressed as the following equation:

$\begin{equation} \label{eq:matrix-orientation-minimization} \min_{\mathbf{\phi}} \|\mathrm{TeacherMixer}(\mathbf{u}) - \mathrm{StudentMixer}_{\boldsymbol{\phi}}(\mathbf{u})\|_F \end{equation}$ where $\phi$ represents the parameters in the layer and $\mathbf{u}$ is the shared input derived from the teacher model. The stage ensures that the student can closely approximate the teacher’s matrix mixer layer which sets a strong foundation for teacher matching in subsequent stages of the MOHAWK process.

For Phi-Mamba: Because the student model uses the Mamba-2 mixer, we initialize the convolution to identity and discarded the nonlinear activation after the convolution to ensure the components upstream of the matrix mixers roughly equivalent to the self-attention layer. The loss calculate was between the self-attention matrix of the teacher and the “unraveled” SSM matrix as shown in Equation \eqref{eq:ssd-matrix-mixer}.

Stage 2: Hidden-State Alignment

After optimizing Equation \eqref{eq:matrix-orientation-minimization} in Stage 1, Stage 2 proceeds to match the outputs of the student and teacher blocks.

$\begin{equation} \label{eq:hidden-state-minimization} \min_{\mathbf{\phi}} \|\mathrm{AttnBlock}(\mathbf{u}) - \mathrm{StudentMixerBlock}_{\boldsymbol{\phi}}(\mathbf{u})\|_2 \end{equation}$ where once again the inputs are the same. Like Stage 1, Stage 2 can be run in parallel. We find that the distance between the layer outputs is strongly correlated with the student model’s ability to recover the teacher model’s knowledge.

For Phi-Mamba: To keep the block architectures as similar as possible, we initialized the Mamba-2 gate to be a value of 1 to simulate Phi’s lack of gating and removed the norm prior to the output projection.

Stage 3: Weight-Transfer and Knowledge Distillation

The final stage aims to fine-tune the entire student model to match the performance of the teacher. This stage is critical for mending the potential discrepancies between post-Stage 2 blocks. We also initialize information dense components of the student model, in particular the MLPs, embedding, and LM head, before fine-tuning the student end-to-end. Given the weight transfer of critical architectural components, the overall block structure of the student mirror that of the teacher model, e.g., our student model has the MLPs and matrix mixer layers in parallel. Finally, we use knowledge distillation loss to encourage the student to imitate the teacher’s distribution:

\[\begin{equation} \min_{\mathbf{\phi}} \mathbf{\mathcal{L}}_{\mathrm{CE}}\big(\mathrm{Teacher}(\mathbf{x}), \mathrm{Student}_{\boldsymbol{\phi}} (\mathbf{x})\big) \end{equation}\]

For Phi-Mamba: We create a new Phi-Mamba block that has the same parallel MLP-matrix mixer layer structure as the original Phi-1.5 block. We copy over the MLP and norm weights, token embeddings, and language model head and pre-head norm as it has been hypothesized that much of a model’s information is stored in these components. We also find that the MLPs can be frozen after the transfer with only a slight decrease in performance but reduce the number of trainable parameters by more than half!

Approximating Self-Attention

With the MOHAWK method we can now distill from any quadratic self-attention model to any model that utilizes a matrix mixer for sequential modeling. But, a caveat is that the performance of the student model is inherently constrained by the expressivity of its matrix mixer. So why did we decide to use the Mamba-2 mixer instead of an alternative like linear attention or gated convolution? In this next section, we will empirically explore Mamba-2’s ability to approximate the self-attention matrix $\text{Softmax}(QK^\top)$ and compare it to some other popular sub-quadratic matrix mixer families. We describe a couple of them below.

Linear Attention and SSD

When describing linear attention matrices, we can utilize the fact that both $Q$ and $K$ are token-dependent projections of some input $x \in \mathbb{R}^{d_{in}}$ onto $\mathbb{R}^{d_{out}}$, and therefore the rank of $Q$ and $K$ are bounded by $\min{ { d_{in}, d_{out} } }$ For multi-head linear attention, $d_{out}$, which corresponds to the head dimension, is typically a small value (e.g., $64$ and $128$ for Phi-1.5 and Llama2-7b-Chat respectively). Thus, we approximate linear attention matrix mixers using causal low-rank matrices $\mathbf{L \circ Q K}^\top$, where $\mathbf{L}$ is a lower-triangular causal mask of 1s, and $\mathbf{Q}$, $\mathbf{K}$ are in $\mathbb{R}^{n \times d}$ with $d \ll n$.

For the multi-head Mamba-2 matrix family, we utilize the state space dual (SSD) layer in a manner similar to the previous linear attention class, but imbuing the causal matrix $\mathbf{L}$ with an $n$-degree rolling multiplicative structure for $\mathrm{SSD}$. This can be seen as a more expressive mask that generalizes the lower-triangular, ones-only causal mask \eqref{eq:ssd-matrix-mixer}.

General Semi-separable and Toeplitz

To approximate the general class of semi-separable matrices (abbreviated as “SSM” in the following table), we utilize balanced truncation. This method is used in the field of time-invariant Dynamical System model reduction and has been modified for use in time-varying systems . Similarly, for the family of Toeplitz matrices, which represent a convolution operation, we apply a causal mask, the same one used for causal low-rank matrices, on top a Toeplitz matrix.

Empirical Approximation

To empirically validate the expressiveness of the four aforementioned families, we sample 1,000 attention matrices, each consisting of 512 tokens, from the Llama2-7B-Chat model on four different datasets. One attention head, and its respective attention matrix, from each layer was chosen at random. Both (causal) low-rank (LR) and SSD matrix families were approximated with 10,000 steps of gradient descent per sample. SSM and Toeplitz were both calculated without using gradient descent using balanced truncation and a simple heuristic respectively. We calculate the Frobenius distance between each “ground truth” self-attention matrix and the approximated matrix of each family.

Matrix Approximation — Self Attention matrix approximation by structured matrix mixers

Given the previous table’s experiment was conducted in a very controlled setting, we further explore the ability of the various families’ abilities to approximate the self-attention matrix within a language model. We replace the self-attention matrix mixers of a Phi-1.5 model with either input-dependent Toeplitz, causal low-rank, or SSD (our Mamba-2 variant) matrix mixers, and ran the second and third stages of our MOHAWK procedure for 1B tokens each.

Matrix Structure Evaluations — Evaluations of various structured matrices on downstream tasks

We find that there is a constant correlation between the self attention approximation abilities (measured via projection distances) of a matrix family and the downstream performance metrics (accuracy) of the matrix mixer integrated into an end-to-end language model. This finding that more expressive matrix mixers lead to more effective models is echoed in .

Next Up

The following section will cover MOHAWK in action, distilling our final Phi-Mamba and Hybrid-Phi-Mamba models, and explore the training laws regarding each stage of MOHAWK.